Пример расчета статически неопределимой системы при растяжении-сжатии

Требуется определить продольные силы в стержне, закрепленном с двух сторон

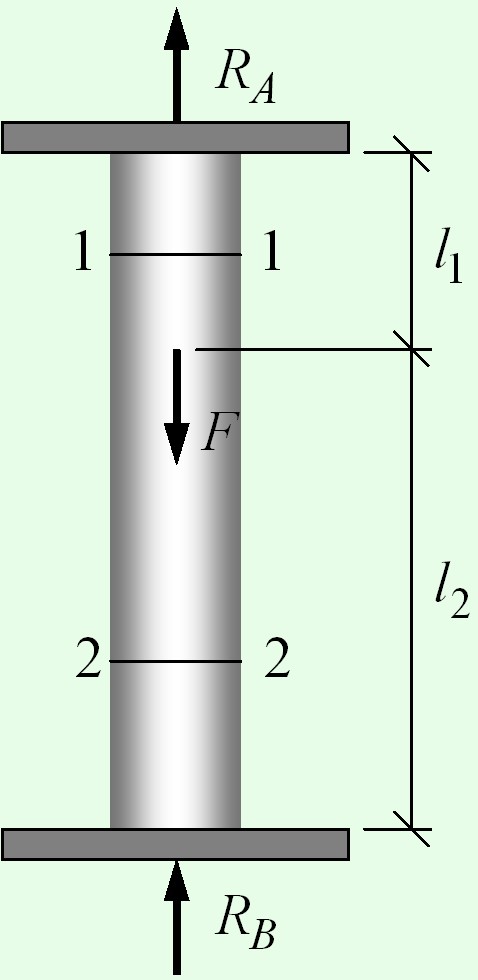
Уравнение равновесия

${R_A} + {R_B} - F = 0$

${N_1} = {R_A}$        ${N_2} =  - {R_B}$

$\Delta {l_1} = \frac{N_1} \cdot {l_1}E \cdot A$      $\Delta {l_2} = \frac{N_2} \cdot {l_2}E \cdot A$

$\Delta {l_1} + \Delta {l_2} = 0$  $\frac{N_1} \cdot {l_1}E \cdot A + \frac{N_2} \cdot {l_2}E \cdot A = 0$   ${N_1} \cdot {l_1} + {N_2} \cdot {l_2} = 0$

$\frac{N_1}{N_2} =  - \frac{l_2}{l_1}$             ${R_A} = {N_1} =  - \frac{l_2}{l_1}{N_2} = \frac{l_2}{l_1}{R_B}$

$\left( { \frac{ l_2}{l_1} + 1} \right){R_B} - F = 0$         ${R_B} = \frac{ { F \cdot {l_1} } } { {l_1} + {l_2} }$      ${R_A} = \frac{ { F \cdot {l_2} } } { {l_1} + {l_2} }$