Ответ: диаметр $d = 13.7 см$, площадь сечения $A = 147см^2$

---

Подробный расчет:
Необходимый минимальный момент сопротивления равен $$W = \frac{M_{max}}{[\sigma]} = \frac{40000}{160} = 250см^3$$
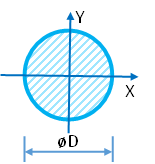
Поскольку момент сопротивления круга $$W=\frac{\pi \cdot d^3}{32}$$ диаметр сечения балки равен $$d = \sqrt[3]{\frac{32\cdot W}{\pi}} = \sqrt[3]{\frac{32\cdot 250}{\pi}} = 13.7 см$$ Площадь сечения балки $$A = \frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 13.7^2}{4} = 147см^2$$

Необходимый минимальный момент сопротивления равен $$W = \frac{M_{max}}{[\sigma]} = \frac{45000}{160} = 281см^3$$
Момент сопротивления прямоугольника $$W=\frac{b \cdot h^2}{6} = \frac{b \cdot (2.5b)^2}{6} = \frac{b^3 \cdot 2.5^2}{6}$$ ширина сечения балки $$b = \sqrt[3]{\frac{6\cdot W}{{hb}^2}} = \sqrt[3]{\frac{6\cdot 281}{2.5^2}} = 6.46 см$$ Высота сечения $$h=6.46\cdot 2.5 = 16.2 см$$ Площадь сечения балки $$A = h \cdot b = 16.2\cdot 6.46 = 105см^2$$

Необходимый минимальный момент сопротивления равен $$W = \frac{M_{max}}{[\sigma]} = \frac{5000}{160} = 31.3см^3$$
Поскольку момент сопротивления кольца (трубы) $$W=\frac{\pi \cdot D^3}{32}(1-\alpha^4)$$ наружный диаметр сечения балки равен $$D = \sqrt[3]{\frac{32\cdot W}{\pi (1-\alpha^4)}} = \sqrt[3]{\frac{32\cdot 31.3}{\pi (1-0.9^4)}} = 9.75 см$$ Внутренний диаметр $$d=9.75\cdot 0.9 = 8.78 см$$ Площадь сечения балки $$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 9.75^2}{4}- \frac{\pi \cdot 8.78^2}{4} = 14.1см^2$$