Метод интегрирования дифференциального уравнения изгиба балки
Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.
$EI\,y"(x) = M(x)$ – полученное дифференциальное уравнение;
$EI\,y'(x) = EI\,\varphi (x) = \int {M(x)} dx + C$ – первый интеграл (уравнение углов поворота);
$EI\,y(x) = \int {EI\,\varphi (x)} dx = \iint {M(x)}dxdx + C\,x + D$ – второй интеграл (уравнение прогибов).
Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).
Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI\,\varphi (0) = C$, а прогиб $EI\,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.
Консольная балка с силой на конце
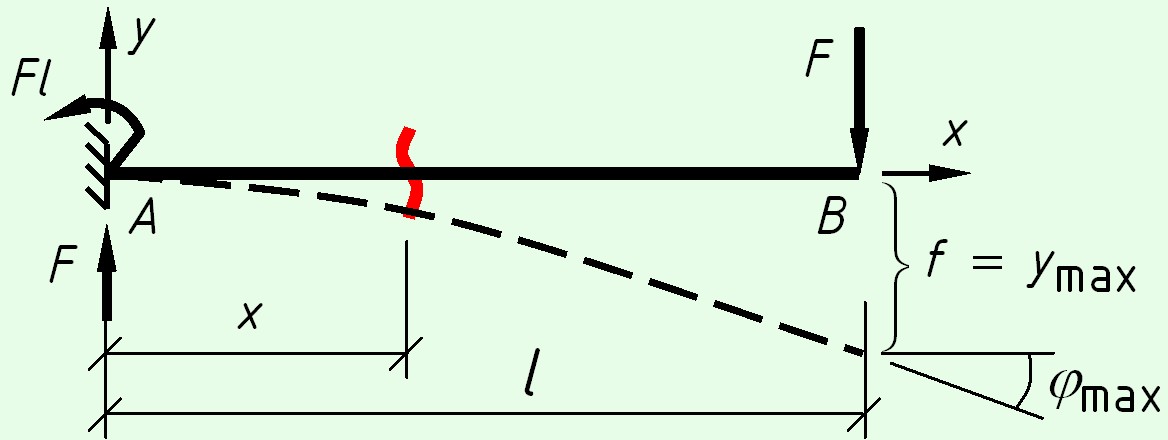
На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F \cdot l$.
Уравнения изгибающих моментов
$M(x) = - Fl + Fx = F(x - l)$
Уравнение углов поворота
$EI\,y'(x) = EI\,\varphi (x) = \int {F(x - l)} dx + C = F(\frac{{{x^2}}}{2} - lx) + C$
Уравнение прогибов
$EI\,y(x) = \int {EI\,\varphi (x)} dx = \int {F(\frac{{{x^2}}}{2} - lx)} \,dx + Cx + D = F(\frac{{{x^3}}}{6} - l\frac{{{x^2}}}{2}) + Cx + D$
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$\left\{ \begin{gathered} EI\,\varphi (0) = F(\frac{{{0^2}}}{2} - l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac{{{0^3}}}{6} - l\frac{{{0^2}}}{2}) + C \cdot 0 + D = 0. \hfill \\ \end{gathered} \right.$
Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
$EI\,y(x) = F(\frac{{{x^3}}}{6} - l\frac{{{x^2}}}{2})$.
Максимальный прогиб будет иметь место при $x = l$
$EI\,y(l) = F(\frac{{{l^3}}}{6} - l\frac{{{l^2}}}{2}) = - F\frac{{{l^3}}}{3}$,
где знак «–» указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = \frac{{F\,{l^3}}}{{3\,EI}}$.
Максимальный угол поворота сечения также будет иметь место при $x = l$
$EI\,\varphi (l) = F(\frac{{{l^2}}}{2} - l \cdot l) = - \frac{{F \cdot {l^2}}}{2}$ или ${\varphi _{\max }} = - \frac{{F\,{l^2}}}{{2\,EI}}$,
знак «–» указывает направление угла поворота – сечение поворачивается по часовой стрелке.
Шарнирно закрепленная балка с силой посередине

На опорах возникают вертикальные реакции ${R_A} = {R_B} = F/2$.
Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид
$M(x) = \frac{F}{2}x$, то есть $EI\,y"(x) = \frac{F}{2}x$, интегрируем дважды
$EI\,y'(x) = \int {\frac{F}{2}x} \,dx + C = F\frac{{{x^2}}}{4} + C$
$EI\,y(x) = \int {F\frac{{{x^2}}}{4}} \,dx + Cx + D = F\frac{{{x^3}}}{{12}} + Cx + D$
Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений
$\left\{ \begin{gathered} EI\,y(0) = F\frac{{{0^3}}}{{12}} + C \cdot 0 + D = 0\,\,\,\,\,\, \Rightarrow \,\,\,\,\,D = 0; \hfill \\ EI\,\varphi \left( {\frac{l}{2}} \right) = F\frac{{{{\left( {\frac{l}{2}} \right)}^2}}}{4} + C = 0\,\,\,\,\, \Rightarrow \,\,\,\,\,C = - \frac{{F\,{l^2}}}{{16}}. \hfill \\ \end{gathered} \right.$
Окончательно функция прогибов для рассматриваемой балки имеет вид
$EI\,y(x) = F\frac{{{x^3}}}{{12}} - \frac{{F{l^2}}}{{16}}x$.
Максимальный прогиб будет иметь место при $x = l/2$
$EI\,y(\frac{l}{2}) = F\frac{{{{(l/2)}^3}}}{{12}} - \frac{{F{l^2}}}{{16}} \cdot \frac{l}{2} = F{l^3}\left( {\frac{1}{{96}} - \frac{1}{{32}}} \right) = F{l^3}\left( {\frac{1}{{96}} - \frac{3}{{96}}} \right) = - \frac{{F\,{l^3}}}{{48}}$,
Стрела прогиба $f = \frac{{F\,{l^3}}}{{48\,EI}}$.
Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).
${\varphi _A} = \varphi (0) = - \frac{{F \cdot {l^2}}}{{16\,EI}}$ или ${\varphi _B} = \varphi (l) = \frac{{F \cdot {l^2}}}{{16\,EI}}$.
Консольная балка с равномерно распределенной нагрузкой
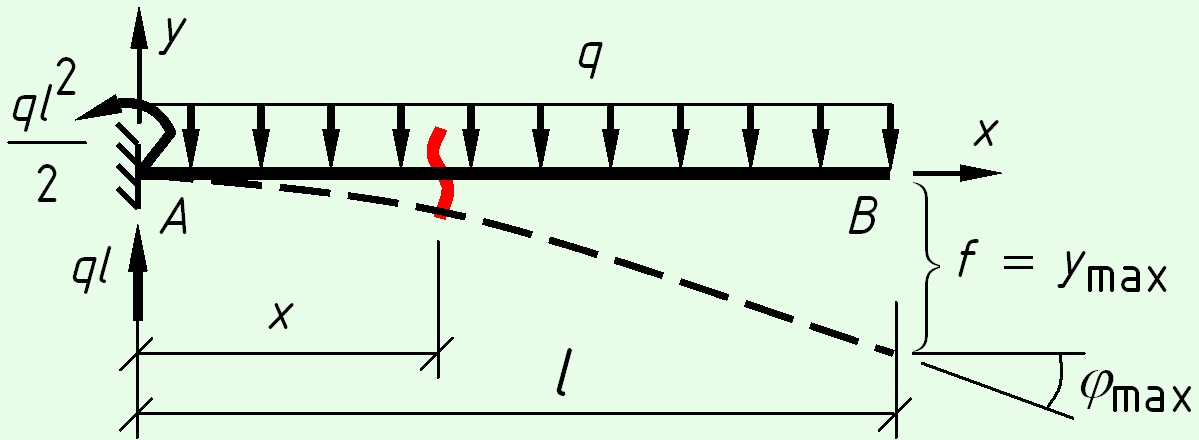
На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = \frac{{q{l^2}}}{2}$.
$M(x) = - \frac{{q{l^2}}}{2} + ql \cdot x - \frac{{q{x^2}}}{2}$, дважды интегрируем
$EI\,y'(x) = q \cdot \left( { - \frac{{{l^2}}}{2}x + \frac{{{x^2}}}{2} - \frac{{{x^3}}}{6}} \right) + C$;
$EI\,y(x) = q \cdot \left( { - \frac{{{l^2}}}{2}\frac{{{x^2}}}{2} + \frac{{{x^3}}}{6} - \frac{{{x^4}}}{{24}}} \right) + Cx + D$.
Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений
$\left\{ \begin{gathered} EI\,y'(0) = F(\frac{{{0^2}}}{2} - l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac{{{0^3}}}{6} - l\frac{{{0^2}}}{2}) + C \cdot 0 + D = 0. \hfill \\ \end{gathered} \right.$
Решение системы уравнений приводит к результату $C = 0$, $D = 0$.
Окончательно функция прогибов для рассматриваемой балки имеет вид
$EI\,y(x) = q \cdot \left( { - \frac{{{l^2}}}{2}\frac{{{x^2}}}{2} + \frac{{{x^3}}}{6} - \frac{{{x^4}}}{{24}}} \right)$.
Максимальный прогиб будет иметь место при $x = l$
$EI\,y(l) = q \cdot \left( { - \frac{{{l^2}}}{2}\frac{{{l^2}}}{2} + \frac{{{l^3}}}{6} - \frac{{{l^4}}}{{24}}} \right) = q{l^4} \cdot \left( { - \frac{6}{{24}} + \frac{4}{{24}} - \frac{1}{{24}}} \right) = - \frac{3}{{24}}q{l^4} = - \frac{1}{8}q{l^4}$,
Стрела прогиба $f = \frac{{q\,{l^4}}}{{8\,EI}}$.
Максимальный угол поворота сечения также будет иметь место при $x = l$
$EI\,\varphi (l) = q \cdot \left( { - \frac{{{l^2}}}{2}l + \frac{{{l^2}}}{2} - \frac{{{l^3}}}{6}} \right) = q{l^3} \cdot \left( { - \frac{1}{2} + \frac{1}{2} - \frac{1}{6}} \right) = - \frac{{q{l^3}}}{6}$ или ${\varphi _{\max }} = - \frac{{q\,{l^3}}}{{6\,EI}}$.
