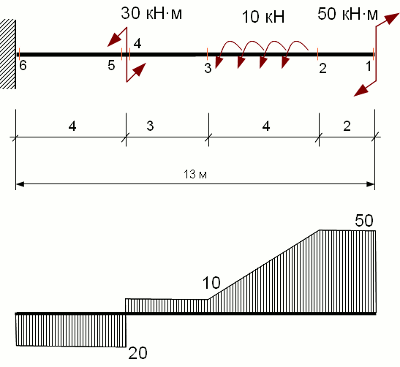
Пример построения эпюры крутящих моментов при кручении вала

Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1 = -30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН.

Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

 Проведем сечение 1. Определим крутящий момент в текущем сечении:

M_к1= M_кв2= 50 кНм

Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M_к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

M_к2 = M_к1 = M_кв2 = 50 кНм

Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

M_к3 = M_кв2 – m₁*4 = 50 – 10*4 = 10 кНм

Аналогично для сечения 4:

M_к4 = M_к3 = 10 кНм

Также для сечения 5:

M_к5= M_к4-M_кв1= 10 – 30 = -20 кНм

Для сечения 6:

M_к6= M_к5 =-20 кНм

По полученным значения строим эпюру крутящих моментов (см. рисунок).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M_к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

• Эпюры крутящих моментов всегда прямолинейные.
• На участке, где нет распределенных моментов, эпюра M_к – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
• Под точкой приложения сосредоточенного момента на эпюре M_к будет скачок на величину этого момента.