Допущения в сопротивлении материалов

При построении теории расчета на прочность, жесткость и устойчивость принимаются допущения, связанные со свойствами материалов и с деформацией тела.

Допущения, связанные со свойствами материалов:

- материал считается однородным (его физико-механические свойства считаются одинаковыми во всех точках;

- материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда). Это допущение дает возможность применять при исследовании напряженно-деформированного состояния тела методы дифференциального и интегрального исчислений, которые требуют непрерывности функции в каждой точке объема тела;

- материал изотропный, то есть его физико-механические свойства в каждой точке одинаковы во всех направлениях. Анизотропные материалы – физико-механические свойства которых изменяются в зависимости от направления (например, дерево);

- материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают).

Допущения, связанные с деформацией тела.

- деформации считаются малыми. Из этого допущения следует, что при составлении уравнений равновесия, а также при определении внутренних сил можно не учитывать деформацию тела. Это допущение иногда называют принципом начальных размеров. Например, рассмотрим стержень, заделанный одним концом в стену и нагруженный на свободном конце сосредоточенной силой.

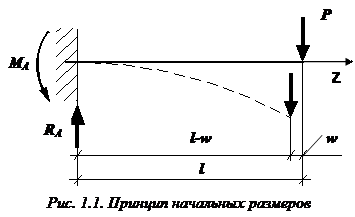
Момент в заделке, определенный из соответствующего уравнения равновесия методом теоретической механики, равен: $M_A = Pl$. Однако прямолинейное положение стержня не является его положением равновесия. Под действием силы (P) стержень изогнется, и точка приложения нагрузки сместится и по вертикали, и по горизонтали. Если записать уравнение равновесия стержня для деформированного (изогнутого) состояния, то истинный момент, возникающий в заделке, окажется равным $M_A = P(l-w)$. Принимая допущение о малости деформаций, мы полагаем, что перемещением (w) можно пренебречь по сравнению с длиной стержня, тогда $M_A = Pl$. Допущение возможно не для всех материалов.

- перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (тело является линейно деформируемым). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности. В основе этого принципа лежит также предположение об обратимости процессов нагрузки и разгрузки.