Рациональные формы сечений балок

Рациональные формы сечения балок

Рациональными формами сечения балок являются такие сечения, которые имеют высокие геометрические характеристики (момент инерции ${I_x}$ – с точки зрения максимальной жесткости и момент сопротивления ${W_x}$ – с точки зрения максимальной прочности) при одинаковой площади сечения $A$. При этом необходимо учесть, что высота сечения ограничена.

Идеальным случаем компоновки сечения является размещение по всей площади верхней и нижней гранях, то есть в местах с максимальными напряжениями.

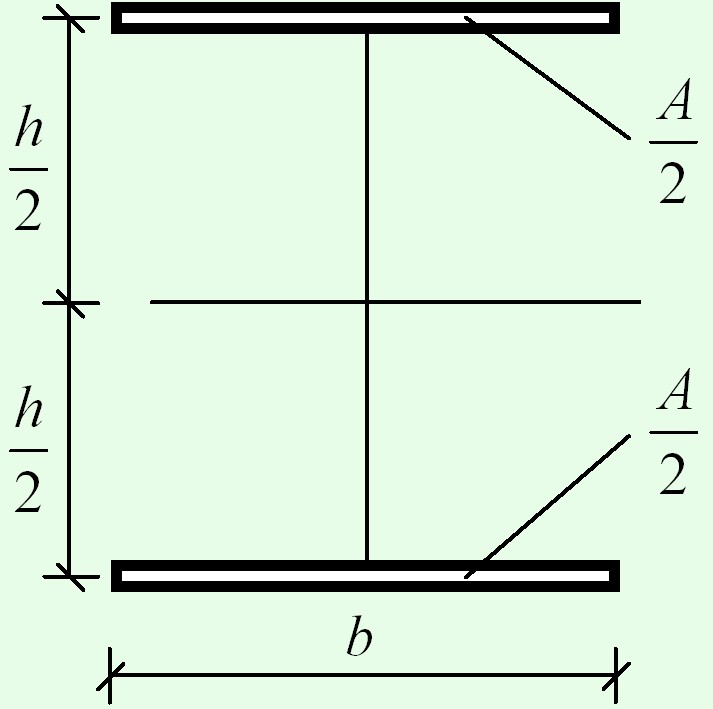
Момент инерции этого сечения

${I_x} = 2 \cdot \frac{A}{2} \cdot {\left( {\frac{h}{2}} \right)^2} = \frac{{A{h^2}}}{4}$

Момент сопротивления

\[{W_x} = \frac{{{I_x}}}{{h/2}} = 0,5 Ah\] – теоретически максимально возможное значение момента сопротивления сечения.

В реальных сечений значение \[{W_x}\] будет меньше и по нему можно судить о рациональности того или иного сечения.

Для прямоугольника \[{W_x} = \frac{{b{h^2}}}{6} = \frac{{bh \cdot h}}{6} = 0,167 Ah\].

Для круга \[{W_x} = \frac{{\pi {d^3}}}{{32}} = \frac{1}{8}\frac{{\pi {d^2}}}{4} \cdot d = 0,125 Ah\].

Для трубчатого сечения при отношении диаметров \[\alpha  = \frac{d}{D} = 0,9\] \[{W_x} = 0,226 Ah\].

Для прокатных профилей

– двутавры \[{W_x} = 0,31..0,34 Ah\]

– швеллеры \[{W_x} = 0,3..0,33 Ah\]

– неравнобокие уголки \[{W_x} = 0,14..0,15 Ah\]

– равнобокие \[{W_x} = 0,12..0,13 Ah\]

Все предыдущие выводы относятся к материалам, которые имеют одинаковые допустимые напряжения на растяжение и сжатие.

Для материалов, для которых допустимые напряжения на растяжение значительно меньше допустимых напряжений на сжатие (такие материалы как чугун) целесообразно распределение материала в сечении сделать так, чтобы максимальные напряжения в сжатой и в растянутой зоне были равны допустимым. Для этого необходимо увеличить площадь сечения растянутой зоны, то есть рациональным будет несимметричный сечение.