Учет собственного веса

Напряжение в призматическом брусе

Собственный вес при расчетах на растяжение-сжатие учитывается для конструкций, вес которых сопоставима со значениями внешних нагрузок. Это могут быть железобетонные колонны, кирпичные простенки и др.

Рассмотрим внутренние усилия и напряжения, возникающие в растянутом стержне при одновременном действии сосредоточенной силы $F$ и собственного веса. Вес стержня определяется как

$Q = \gamma  \cdot V = \gamma  \cdot A \cdot l$,

где $\gamma $ – удельный вес материала [кН/м³], $V$, $A$, $l$ – об’объем, площадь сечения и длина стержня соответственно. Удельный вес эт’связана с плотностью материала $\gamma  = g \cdot \rho $, где $g \approx 10$ м/с², $\rho $– плотность.

 

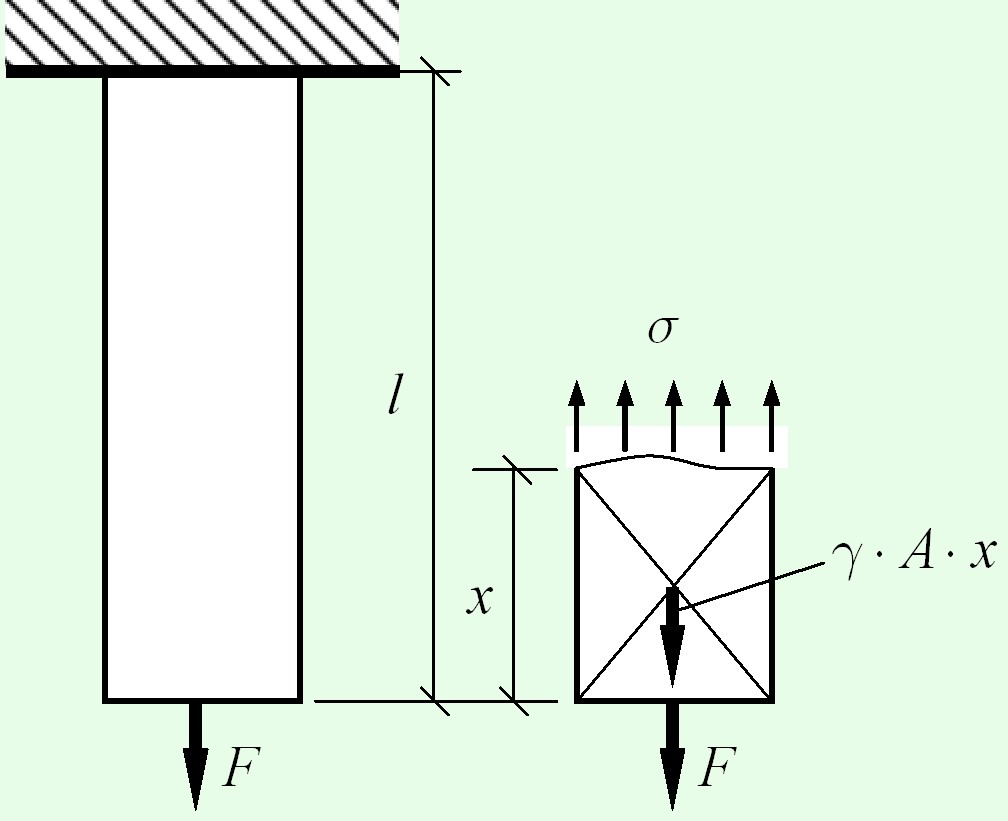
Продольная сила, возникающая в сечении И – И

$N = F + \gamma  \cdot A \cdot x$

Напряжение при учете собственного веса

$\sigma  = \frac{N}{A} = \frac{F}{A} + \gamma  \cdot x$

Наибольшее напряжение возникает в верхнем сечении и условие прочности примет вид

${\sigma _{\max }} = \frac{F}{A} + \gamma  \cdot l \leqslant \left[ \sigma  \right]$

Подбор площади сечения с учетом собственного веса

${A_{\min }} = \frac{F}{{\left[ \sigma  \right] - \gamma  \cdot l}}$

Брус равного сопротивления

Брусом равного сопротивления называется брус, в котором напряжения по длине не меняются и, как правило, равны допустимым напряжением.

Вполне понятно, чтобы удовлетворить таким условиям, площадь сечения бруса должна меняться в соответствии с изменением продольной силы. Рассмотрим бесконечно малый элемент бруса (рис.) длиной $dx$. Нижний сечение этого элемента имеет площадь $A$. Продольная сила в нем равна $[\sigma ] \cdot A$. Продольная сила в верхнем сечении увеличивается на величину веса элемента, то есть на $dN = \gamma  \cdot dV = \gamma  \cdot A \cdot dx$. Соответственно площадь увеличивается на величину $dA = \frac{{dN}}{{[\sigma ]}}$.

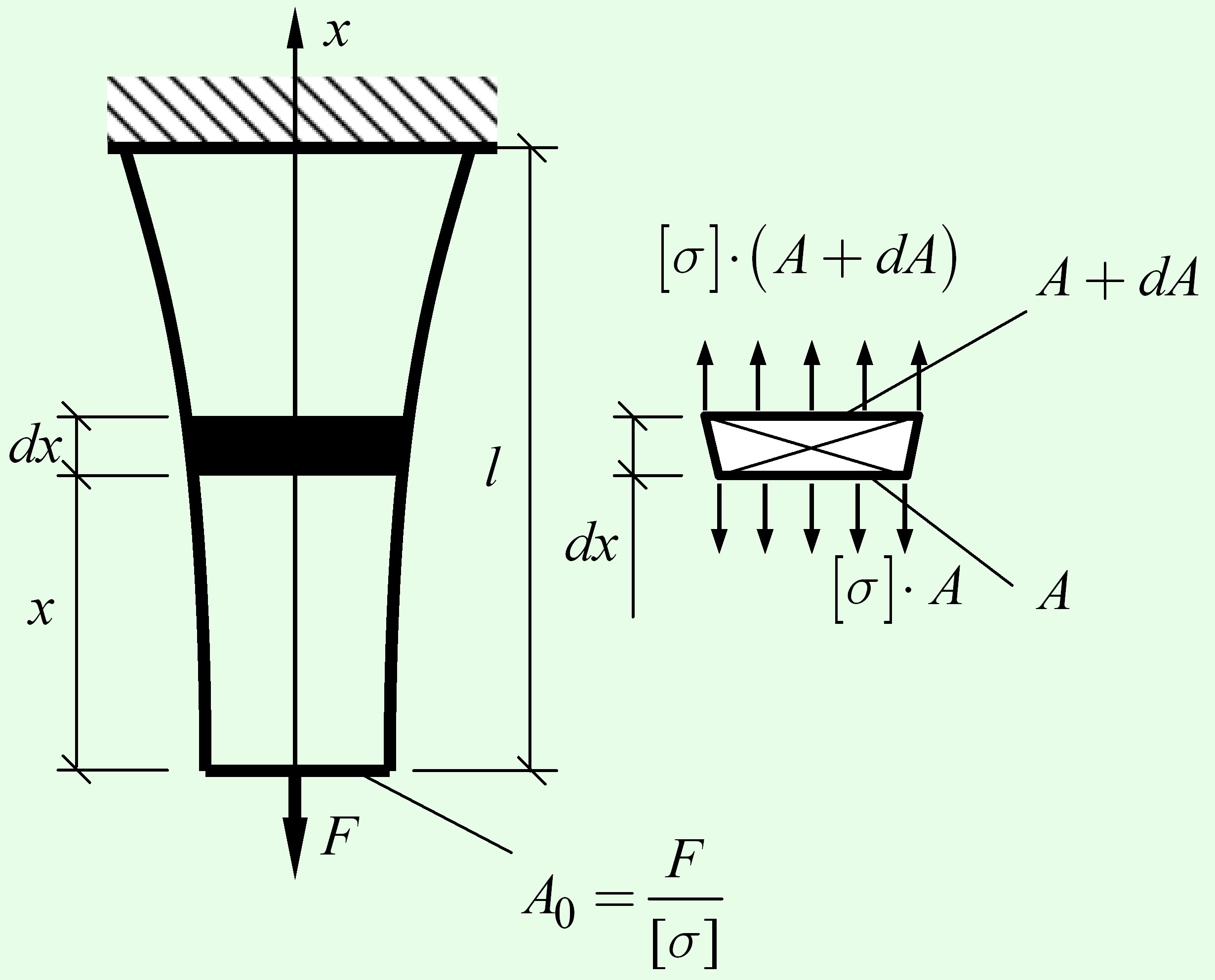
Таким образом,

$dN = \gamma  \cdot A \cdot dx = dA \cdot [\sigma ]$,

$\frac{{dA}}{A} = \frac{\gamma }{{\left[ \sigma  \right]}} \cdot dx$,  \[\int {\frac{{dA}}{A}}  = \int {\frac{\gamma }{{\left[ \sigma  \right]}} \cdot dx} \], $\ln \left( A \right) = \frac{\gamma }{{\left[ \sigma  \right]}} \cdot x + C$.

В нижнем сечении, где продольная сила $N = F$, площадь сечения должна быть

${A_0} = \frac{F}{{[\sigma ]}}$.

Тогда

$\ln \left( {{A_0}} \right) = \frac{\gamma }{{\left[ \sigma  \right]}} \cdot 0 + C\,\,\,\, \Rightarrow \,\,\,\,\,C = \ln \left( {{A_0}} \right)$,

$\ln \left( A \right) - \ln \left( {{A_0}} \right) = \frac{\gamma }{{\left[ \sigma  \right]}} \cdot x$,

$\frac{A}{{{A_0}}} = {e^{\frac{\gamma }{{\left[ \sigma  \right]}} \cdot x}}$.

то Есть, для обеспечения одинаковых напряжений по длине стержня, площадь сечения должна изменяться по экспоненциальной зависимостью

$A(x) = {A_0} \cdot e{\,^{\frac{\gamma }{{\left[ \sigma  \right]}} \cdot x}}$. 

Ступенчатый брус

Брус равного сопротивления неудобен для изготовления, поэтому для выравнивания напряжений используют ступенчатое изменение сечения по длине. При этом количество и длину ступеней определяют в зависимости от ситуации, а необходимую площадь сечения каждой ступени назначают из условия прочности как для призматического бруса. Например, для трехступенчатого бруса с нагрузкой на его конце расчет площадей сечения проводится, как показано на рис.6.3.

Деформации от собственного веса

Напряжение при учете только собственного веса для призматического бруса

$\sigma  = \frac{{\gamma  \cdot A \cdot x}}{A} = \gamma  \cdot x$.

По закону Гука

\[\varepsilon  = \frac{\sigma }{E} = \frac{{\gamma x}}{E}\]

\[\Delta l = \int\limits_0^l {d\Delta l}  = \int\limits_0^l {\frac{\gamma }{E} \cdot dx}  = \frac{\gamma }{E} \cdot \left. {\frac{{{x^2}}}{2}} \right|_0^l = \frac{\gamma }{E} \cdot \frac{{{l^2}}}{2} = \frac{{Q \cdot l}}{{2 \cdot EA}}\].

Если на стержень, кроме собственного веса $Q$ действует сила $F$, удлинение будет определяться по формуле

$\Delta l = \frac{{N\,l}}{{EA}} + \frac{{Q\,l}}{{2\,EA}}$.

Деформации бруса равного сопротивления определяются проще, потому что напряжение во всех сечениях одинаковы $\sigma  = \left[ \sigma  \right] = const$, тогда по закону Гука

$\varepsilon  = \frac{{\left[ \sigma  \right]}}{E} = const$,

$\Delta l = \varepsilon  \cdot l = \frac{{\left[ \sigma  \right]}}{E} \cdot l$