Сдвиг. Срез

Сдвиг – вид деформации стержня, при котором соседние поперечные сечения смещаются друг относительно друга в поперечном направлении.

Срезом, как правило, называют процесс разрушения стержня при смещении (когда одна часть стержня отделяется от другой в поперечном направлении).

Напряжения и деформации, закон Гука при сдвиге

При смещении возникает поперечная сила $Q$ – внутреннее усилие, которое определяется как сумма всех сил, действующих по одну сторону от рассматриваемого сечения в поперечном направлении. Таким образом, поперечная сила действует поперек оси стержня и параллельно поперечного сечения. Напряжение $\tau $, вызванные поперечной силой $Q$, также направлены параллельно (по касательной) к сечению. Такие напряжения называются касательными. Считается, что касательные напряжения при сдвиге распределяются по сечению равномерно, поэтому

$$\tau  = \frac{Q}{A}$$

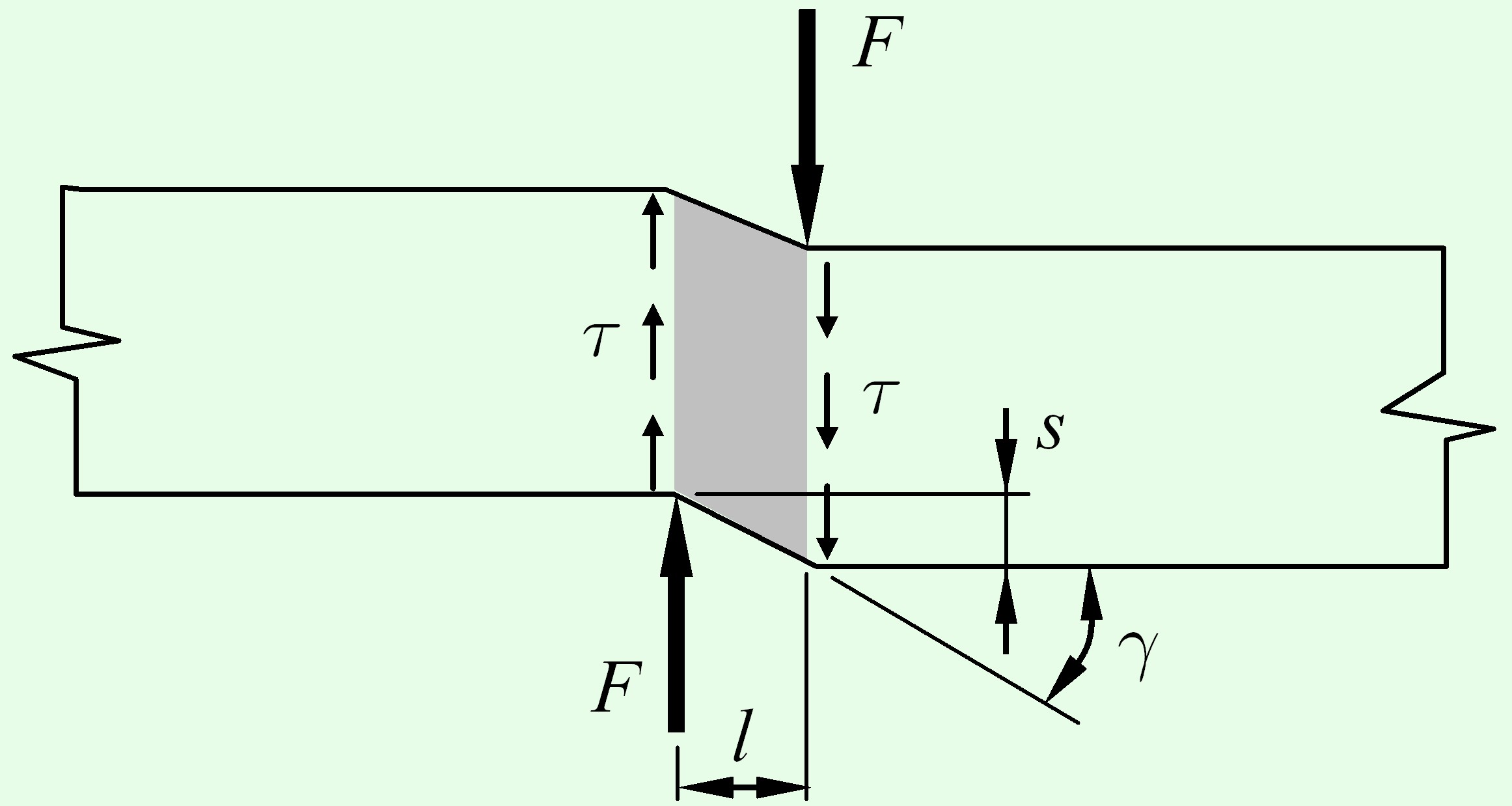
Абсолютным сдвигом $s$ называется смещение сечения в поперечном направлении.

Относительный сдвиг – отношение абсолютного сдвига $s$ до длины рассматриваемой части стержня $l$.

$tg\,\gamma  = \frac{s}{l}$.

Угол $\gamma $ называется углом смещения, или деформацией сдвига.

Поскольку величина абсолютного сдвига $s$ намного меньше величины $l$, то $tg\,\gamma  \approx \gamma$.

Так, как и при растяжении-сжатии, при сдвиге существует линейная зависимость между напряжениями и относительными деформациями. Эта зависимость носит название закон Гука при сдвиге.

$$\tau  = G \cdot \gamma $$,

где $G$ – модуль сдвига, или модуль упругости второго рода [Па, МПа].

Таким образом, модуль упругости $E$, модуль сдвига $G$ и коэффициент Пуассона $\nu $ в полной мере характеризуют деформативные свойства материалов.

Оказывается, между этими тремя характеристиками существует зависимость

$$G = \frac{E}{{2\left( {1 + \nu } \right)}}$$

она справедлива для любого материала, который имеет одинаковые свойства во всех направлениях (такие материалы называют изотропными).

Так, для сталей $G = \frac{{2,1 \cdot {{10}^5}}}{{2(1 + 0,3)}} = 0,8 \cdot {10^5}$МПа.