Объемное напряженное состояние

Объемным напряженным состоянием называют напряженное состояние, которое можно представить в виде трех ненулевых главных напряжений. Это напряженное состояние является общим случаем напряженного состояния тела в точке.

Обобщенный закон Гука

Напомним, что при одноосному растяжению или сжатию возникают деформации – продольные (в направлении действия силы) $\varepsilon  = \sigma /E$ и поперечные (в двух других перпендикулярных направлениях) $\varepsilon ' =  - \nu  \cdot \varepsilon  =  - \nu \sigma /E$.

В случае действия трех главных напряжений ${\sigma _1}$, ${\sigma _2}$ и ${\sigma _3}$ от каждого из них будут возникать продольные и поперечные деформации. Например, от напряжения ${\sigma _2}$ будет возникать продольная деформация в направлении 2, которая равна ${\varepsilon _2} = {\sigma _2}/E$ и поперечные деформации в направлениях 1 и 3 ${\varepsilon _1} = {\varepsilon _3} =  - \nu  \cdot {\sigma _2}/E$. Таким образом, деформации в направлении главных осей от системы трех главных напряжений будут определяться так

$\begin{gathered} {\varepsilon _1} = \frac{1}{E}\left( {{\sigma _1} - \nu ({\sigma _2} + {\sigma _3})} \right) \hfill \\ {\varepsilon _2} = \frac{1}{E}\left( {{\sigma _2} - \nu ({\sigma _1} + {\sigma _3})} \right) \hfill \\ {\varepsilon _3} = \frac{1}{E}\left( {{\sigma _3} - \nu ({\sigma _1} + {\sigma _2})} \right) \hfill \\ \end{gathered} $  – обобщенный закон Гука.

Объемная деформация. Объемный закон Гука

Определим изменение объема тела, которое находится в условиях объемного напряженного состояния.

Объем элементарного куба сторонами $dx$, $dy$ и $d$

${V_0} = dx \cdot dy \cdot d$.

После деформации, когда длина сторон куба изменилась на величину $\Delta x$, $\Delta y$ и $\Delta z$, об’ем

\[\begin{gathered}   {V_1} = (dx + \Delta x) \cdot (dy + \Delta y) \cdot (dz + \Delta z) =  \hfill \\   dx \cdot dy \cdot d + dx \cdot dy \cdot \Delta z + dx \cdot \Delta y \cdot d + \underline {\underline {dx \cdot \Delta y \cdot \Delta z} }  +  \hfill \\    + \Delta x \cdot dy \cdot d + \underline {\underline {\Delta x \cdot dy \cdot \Delta z} }  + \underline {\underline {\Delta x \cdot \Delta y \cdot d} }  + \underline {\underline {\underline {\Delta x \cdot \Delta y \cdot \Delta z} } }  \hfill \\ \end{gathered} \]

Поскольку удлинения являются ничтожно малыми по сравнению с размерами элемента (например, $\Delta x <  < dx$), то в данной формуле можно пренебречь слагаемыми, которые являются бесконечно малыми второго и третьего порядка (подчеркнуты).

Абсолютное изменение о’объема

\[\Delta V = {V_1} - {V_0} = dx \cdot dy \cdot \Delta z + dx \cdot \Delta y \cdot d + \Delta x \cdot dy \cdot d\]

Относительное изменение о’объема

\[{\varepsilon _v} = \frac{{\Delta V}}{{{V_0}}} = \frac{{dx \cdot dy \cdot \Delta z + dx \cdot \Delta y \cdot d + \Delta x \cdot dy \cdot d}}{{dx \cdot dy \cdot d}} = \frac{{\Delta x}}{{dx}} + \frac{{\Delta y}}{{dy}} + \frac{{\Delta z}}{{d}} = {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}\].

Если подставить вдносні деформации из обобщенного закона Гука, получим

 

\[\begin{gathered} {\varepsilon _v} = {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _2} = \frac{1}{E}\left( {{\sigma _1} - \nu {\sigma _2} - \nu {\sigma _3} + {\sigma _2} - \nu {\sigma _1} - \nu {\sigma _3} + {\sigma _3} - \nu {\sigma _1} - \nu {\sigma _2}} \right) =  \hfill \\  = \frac{1}{E}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3} - 2\nu  \cdot \left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)} \right) = \frac{{1 - 2\nu }}{E}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right) \hfill \\ \end{gathered} \]

\[{\varepsilon _v} = \frac{{1 - 2\nu }}{E}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)\] – об’емкий закон Гука.

Если среднее арифметическое значение главных напряжений , то объемный закон Гука можно записать так

,

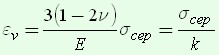где \[k = \frac{E}{{3\left( {1 - 2\nu } \right)}}\] – модуль объемной деформации, а

\[{\varepsilon _v} = \frac{{{\sigma _1} + {\sigma _2} + {\sigma _3}}}{k}\].

Потенциальная энергия деформации

При деформации любого тела тратится определенное количество энергии, которая может превращаться в тепловую (при пластическом деформировании), или накапливаться внутри тела в виде внутренней энергии деформации (при упругом деформировании). В последнем случае при разгрузке тела эта накопленная внутренняя энергия выполняет работу.

Определим внутреннюю энергию, которая накапливается в стержне, растянутом силой $F$. Удлинение, которую приобретет стержень, определится по закону Гука

$\Delta l = \frac{{F \cdot l}}{{EA}}$.

Работа, затраченные силой $F$ на перемещении $\Delta l$, определяется как $F \cdot \Delta l$, но это справедливо только в случае, когда сила является неизменной в процессе удлинения стержня. На самом деле, значение силы изменяется от 0 до \[F\] пропорционально удлинению. Поэтому в случае деформирования тела работа, затраченные на деформирование, а вместе с ней и потенциальная энергия деформации будет определяться как

\[U = \frac{{F \cdot \Delta l}}{2} = \frac{F}{2} \cdot \frac{{F \cdot l}}{{EA}} = \frac{{{F^2} \cdot l}}{{2EA}}\].

Удельная потенциальная энергия, которая накапливается в единице об’объема материала)

\[u = \frac{U}{V} = \frac{{F \cdot \Delta l}}{{2 \cdot A \cdot l}} = \frac{1}{2} \cdot \frac{F}{A} \cdot \frac{{\Delta l}}{l} = \frac{1}{2} \cdot \sigma  \cdot \varepsilon  = \frac{{\sigma  \cdot \varepsilon }}{2} = \frac{{{\sigma ^2}}}{{2E}}\].

В случае действия касательных напряжений аналогично

\[u = \frac{{\tau  \cdot \gamma }}{2} = \frac{{{\tau ^2}}}{{2G}}\].

В случае о’объемного напряженного состояния

 

\[\begin{gathered} u = \frac{{{\sigma _1} \cdot {\varepsilon _1}}}{2} + \frac{{{\sigma _2} \cdot {\varepsilon _2}}}{2} + \frac{{{\sigma _3} \cdot {\varepsilon _3}}}{2} =  \hfill \\   = \frac{1}{{2E}}\left( {{\sigma _1} \cdot \left( {{\sigma _1} - \nu ({\sigma _2} + {\sigma _3})} \right) + {\sigma _2} \cdot \left( {{\sigma _2} - \nu ({\sigma _1} + {\sigma _3})} \right) + {\sigma _3} \cdot \left( {{\sigma _3} - \nu ({\sigma _1} + {\sigma _2})} \right)} \right) \hfill \\ \end{gathered} \]

После упрощения имеем

\[u = \frac{1}{{2E}}\left( {\sigma _1^2 + \sigma _2^2 + \sigma _3^2 - 2\nu  \cdot \left( {{\sigma _1}{\sigma _2} + {\sigma _2}{\sigma _3} + {\sigma _1}{\sigma _3}} \right)} \right)\].

При этом можно отдельно выделить потенциальную энергию, которая соответствует изменению о’объема тела

и изменении формы тела

.

 

Зависимости между модулем упругости E и модулем сдвига G

Рассмотрим частный случай плоского напряженного состояния – чистый сдвиг, при котором на некоторых площадках возникают только касательные напряжения \[\tau \]. Ранее показано, что при чистом сдвиге главными площадками являются площадки, которые находятся под углом 45 в рассматриваемых. Главные напряжения при этом

 

\[\begin{gathered}  {\sigma _1} = \tau  \hfill \\  {\sigma _2} = 0 \hfill \\   {\sigma _3} =  - \tau  \hfill \\ \end{gathered} \]

Тогда потенциальная энергия деформации

\[u = \frac{1}{{2E}}\left( {\tau _{}^2 + 0 + \tau _{}^2 - 2\nu  \cdot \left( {0 + 0 - {\tau ^2}} \right)} \right) = \frac{{2 + 2\nu }}{{2E}}{\tau ^2} = \frac{{1 + \nu }}{E}{\tau ^2}\].

Если рассмотреть ту же самую энергию на площадках, где возникают только касательные напряжения, то

\[u = \frac{{{\tau ^2}}}{{2G}}\].

Отсюда \[\frac{{1 + \nu }}{E}{\tau ^2} = \frac{{{\tau ^2}}}{{2G}}\], то есть между модулем упругости E, модулем сдвига G и коэффициентом Пуассона $\nu$ существует взаимозависимость

\[G = \frac{E}{{2\left( {1 + \nu } \right)}}\]

которая справедлива для всех изотропных материалов (материалов, деформівні свойства которых одинаковы во всех направлениях).