Плоское напряженное состояние

Напряженное состояние тела в точке

Напряженным состоянием тела в точке называется совокупность напряжений на всех площадках, проходящих через данную точку тела.

В общем случае напряженное состояние тела выглядит так.

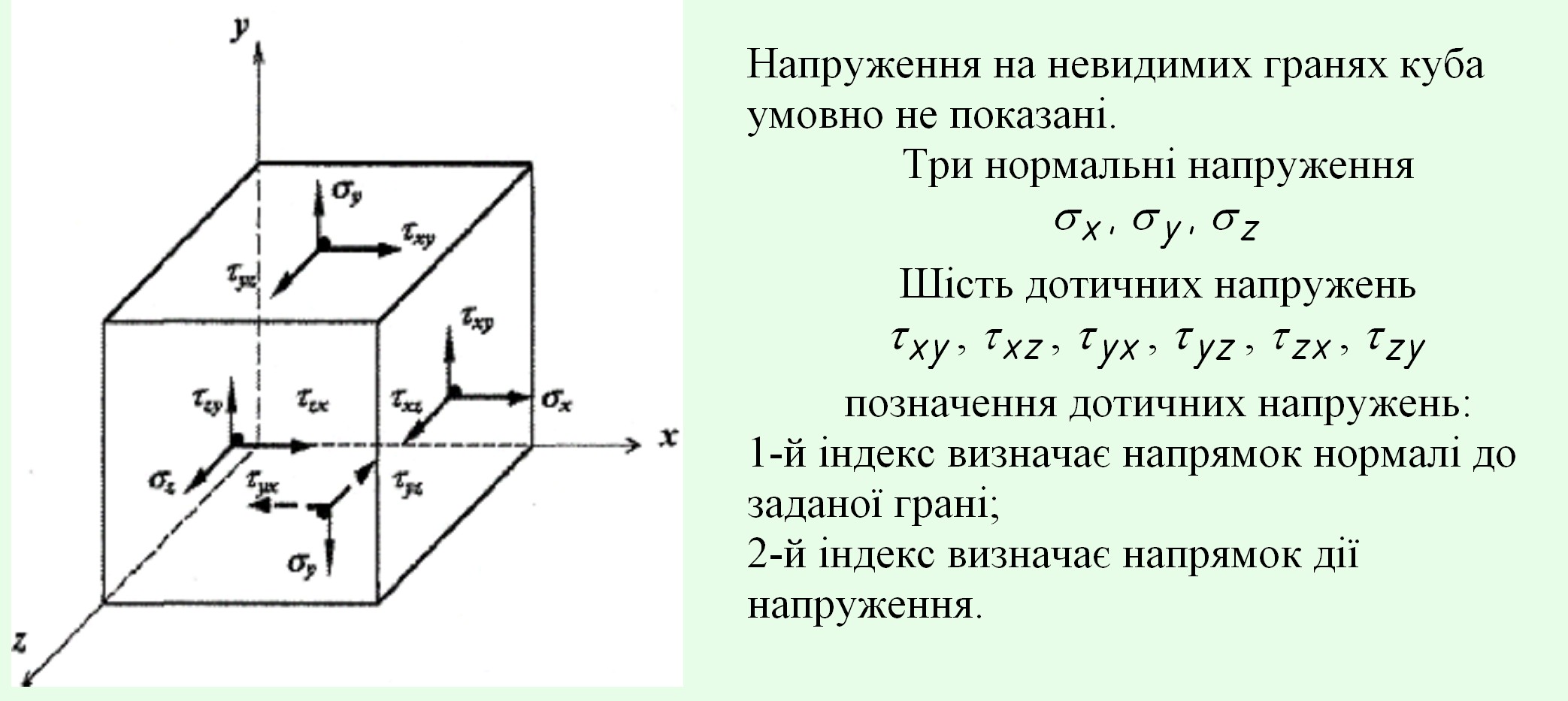
Таким образом, на гранях элементарного куба действует 9 независимых компонентов напряжений, совокупность которых напряжений носит название тензора напряжений.

Возвращая элементарный куб, будем получать изменение напряженного состояния вокруг точки, то есть изменение действующих напряжений как по величине, так и по направлению.

Изменение напряжений в точке при повороте площадок

Рассмотрим равновесие элементарной треугольной призмы толщиной $b = 1$, выделенной вокруг рассматриваемой точки под действием напряжений на вертикальной, горизонтальной и наклонной площадках (Рис. 11.2). Обозначим длину наклонной площадки $ds$. Ее площадь $dA = b \cdot ds = ds$. Рівнодійні напряжений на площадках будут определяться как напряжение, помноженные на площадь площадки.

Запишем уравнение суммы моментов сил относительно точки А.

\[\Sigma {M_0} = {\tau _{xy}} \cdot ds \cdot \cos \alpha  \cdot \frac{{ds \cdot \sin \alpha }}{2} + {\tau _{yx}} \cdot ds \cdot \sin \alpha  \cdot \frac{{ds \cdot \cos \alpha }}{2} = 0\]

${\tau _{xy}} =  - {\tau _{yx}} = \tau $ – закон парности касательных напряжений.

На взаимно перпендикулярных площадках возникают касательные напряжения одинаковы по величине и противоположны по знаку.

Поскольку это правило выполняется всегда, касательные напряжения на взаимно перпендикулярных площадках обозначаются одинаково. Общепринятое правило знаков касательных напряжений показано на рисунке.

Положительное направление касательных напряжений

$\Sigma n =  - {\sigma _гор}ds\cos _{}^2\alpha  - {\sigma тп}ds\sin _{}^2\alpha  + \tau ds\cos \alpha \sin \alpha  + \tau ds\sin \alpha \cos \alpha  + {\sigma _\alpha }ds = 0$

После упрощений получим

\[{\sigma _\alpha } = {\sigma _гор}\cos _{}^2\alpha  + {\sigma тп}\sin _{}^2\alpha  - \tau \sin 2\alpha \]

Нормальные напряжения на площадке, перпендикулярной к указанной наклонной площадки

 

\[\begin{gathered}
\sigma _\alpha ^{}` = {\sigma _{90 + \alpha }} = {\sigma _гор}\cos _{}^2\left( {90 + \alpha } \right) + {\sigma тп}\sin _{}^2\left( {90 + \alpha } \right) + \tau \sin 2\left( {90 + \alpha } \right) =  \hfill \\
= {\sigma _гор}\sin _{}^2\alpha  + {\sigma тп}\cos _{}^2\alpha  + \tau \sin 2\alpha . \hfill \\
\end{gathered} \]

Запишем уравнение суммы всех сил, действующих вдоль касательной к наклонной площадки.

$\Sigma t =  - {\sigma _гор}ds\cos \alpha  \cdot \sin \alpha  + {\sigma тп}ds\sin \alpha  \cdot \cos \alpha  - \tau ds\cos _\alpha ^2 + \tau ds\sin _\alpha ^2 + {\tau _\alpha }ds = 0$

\[{\tau _\alpha } = \frac{{{\sigma _гор} - {\sigma тп}}}{2}\sin 2\alpha  + \tau \cos 2\alpha \]

Таким образом, напряжения на произвольных площадках, наклоненных к заданным под углом $\alpha $ против часовой стрелки, будут определяться так:

В полученных формулах наблюдается полная аналогия с формулами для определения моментов инерции при повороте осей.

Определим нормальные напряжения на экстремум при изменении угла $\alpha $. Для этого производную прирівняємо к нулю.

\[2\tau \cos 2\alpha  = \left( {{\sigma тп} - {\sigma _гор}} \right) \cdot \sin 2\alpha \]

\[tg\,2\alpha  = \frac{{2\,\tau }}{{{\sigma тп} - {\sigma _гор}}}\].                                        

Следовательно, напряжение ${\sigma _\alpha }$ имеют экстремальное значение на площадке, которая находится под углом $\alpha $, определенным по (11.4). Аналогично можно показать, что и напряжение ${\sigma _\alpha }'$ имеют то же свойство. Кроме этого, из формулы (11.3) видно, что касательные напряжения на этих площадках равны нулю.

Главными площадками называют площадки, на которых действуют экстремальные нормальные напряжения, а касательные напряжения равны нулю. Главными напряжениями называют нормальные напряжения на главных площадках.

Угол поворота главных площадок

\[tg2{\alpha _0} = \frac{{2\tau }}{{{\sigma тп} - {\sigma _гор}}}\]

При этом

\[{\sigma _\alpha } + \sigma {'_\alpha } = {\sigma _гор} + {\sigma тп}\]

В общем (об’емком) случая напряженного состояния в точке возникает три взаимно перпендикулярных главных напряжения. По величине этих напряжений можно судить о прочности материала.

Главные напряжения принято называть ${\sigma _1}$, ${\sigma _2}$,${\sigma _3}$, причем обязательно’обязательно должно выполняться условие ${\sigma _1} \geqslant {\sigma _2} \geqslant {\sigma _3}$. То есть, если три главные напряжения равны 25, – 42 и 0 МПа, то ${\sigma _1}$ = 25 МПа, ${\sigma _2}$ = 0, ${\sigma _3}$ = – 40 МПа.

Отдельные случаи напряженного состояния

в Зависимости от того, сколько главных напряжений отлично от нуля различают три вида напряженного состояния тела в точке: линейный, плоский и объемный.

1. в Линейное напряженное состояние – из трех главных напряжений отличным от нуля будет только одно.

${\sigma _гор} = \sigma $

${\sigma _\alpha } = {\sigma _гор} \cdot \cos _\alpha ^2$

${\tau _\alpha } = \frac{\sigma }{2} \cdot \sin 2\alpha $                 ${\tau _{\max }} = \frac{\sigma }{2}$          при 45.  (линии Чернова, чугун под 45)

2. в Чистый сдвиг

${\sigma _гор} = \sigma $                  ${\sigma тп} =  - \sigma $          $\tau  = 0$

${\sigma _{45}} = 0$               $\sigma {'_{45}} = 0$              ${\tau _{45}} = \sigma $

Чистый сдвиг – случай сдвига, когда возникают только касательные напряжения, а нормальные равны нулю.

3. в Однородное напряженное состояние.

${\sigma _гор} = \sigma $                  ${\sigma тп} = \sigma $          $\tau  = 0$

${\sigma _\alpha } = \sigma $               $\sigma {'_\alpha } = \sigma $              ${\tau _\alpha } = 0$

Однородное напряженное состояние – напряженное состояние, при котором на всех площадках возникают только нормальные напряжения.