Продольная сила. Метод сечений. Эпюры продольных сил

Внутренние силы при растяжении-сжатии

Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие (продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.

Продольная сила при растяжении считается положительной, при сжатии – отрицательной.

Пример определения внутренних сил.

Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.

 

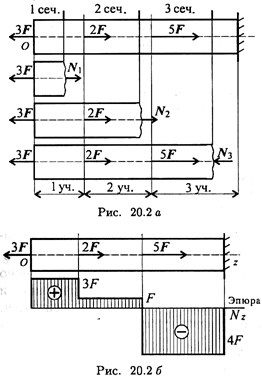
Участком нагружения считают часть бруса между внешними силами.

На представленном рисунке 3 участка нагружения.

Воспользуемся методом сечений и определим внут­ренние силовые факторы внутри каждого участка.

Расчет начинаем со свободного конца бруса, что­бы не определять величины реакций в опорах.

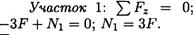
Продольная сила положи­тельна, участок 1 растянут.

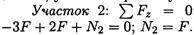
Продольная сила положительна, участок 2 растянут.

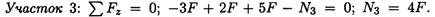
Продольная сила отрицательна, участок 3 сжат.

Полученное значение N₃ равно реакции в заделке.

Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси.

Нулевая линия про­водится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.

В пределах одного участка значение силы не меняется, поэто­му эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Напряжения. Действующие и допускаемые напряжения

Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.

Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными.

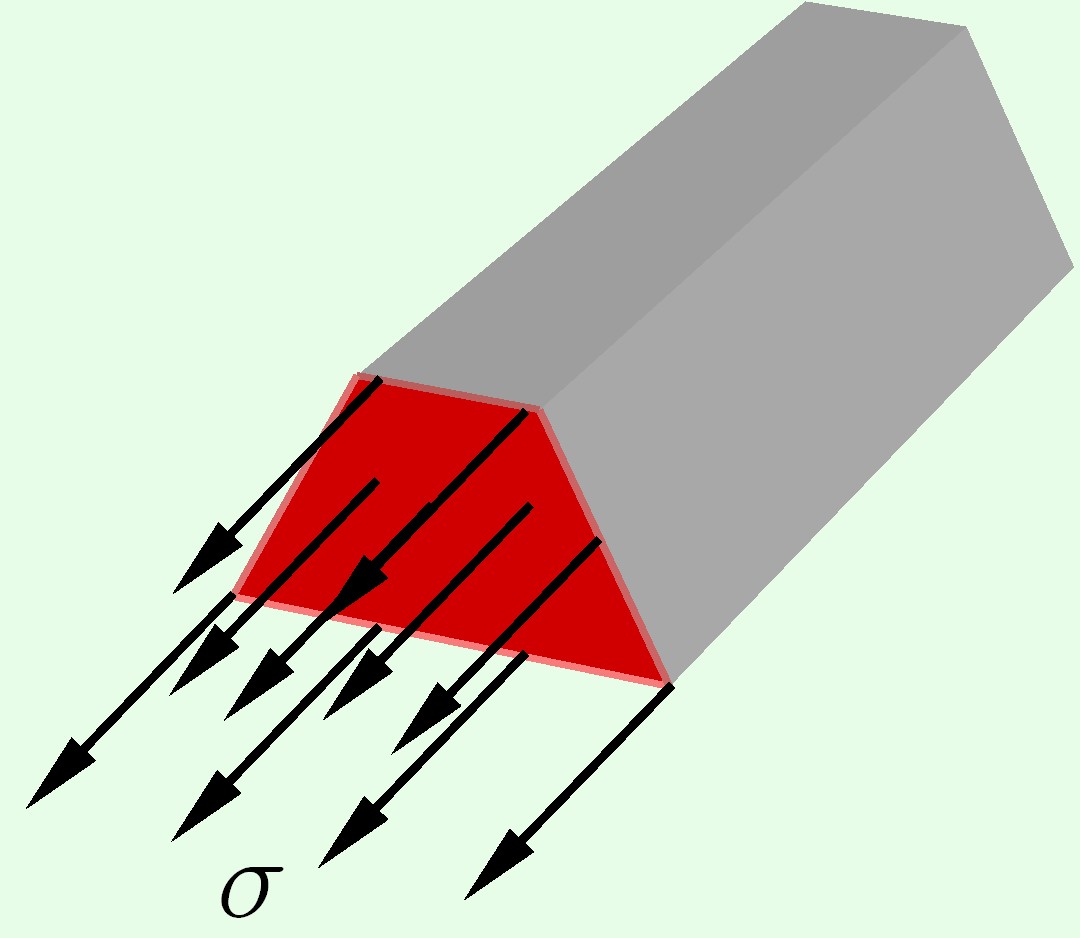
$\sigma  = \frac{N}{A}$

Единицы измерения напряжений - Па, кПа, МПа.

Знаки напряжений принимают так, как и для продольной силы.

Действующие напряжения - напряжения, которые возникают в рассматриваемом сечении.

Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.

Допускаемые напряжения $\left[ \sigma  \right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.

Принцип Сен-Венана: в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.

то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.

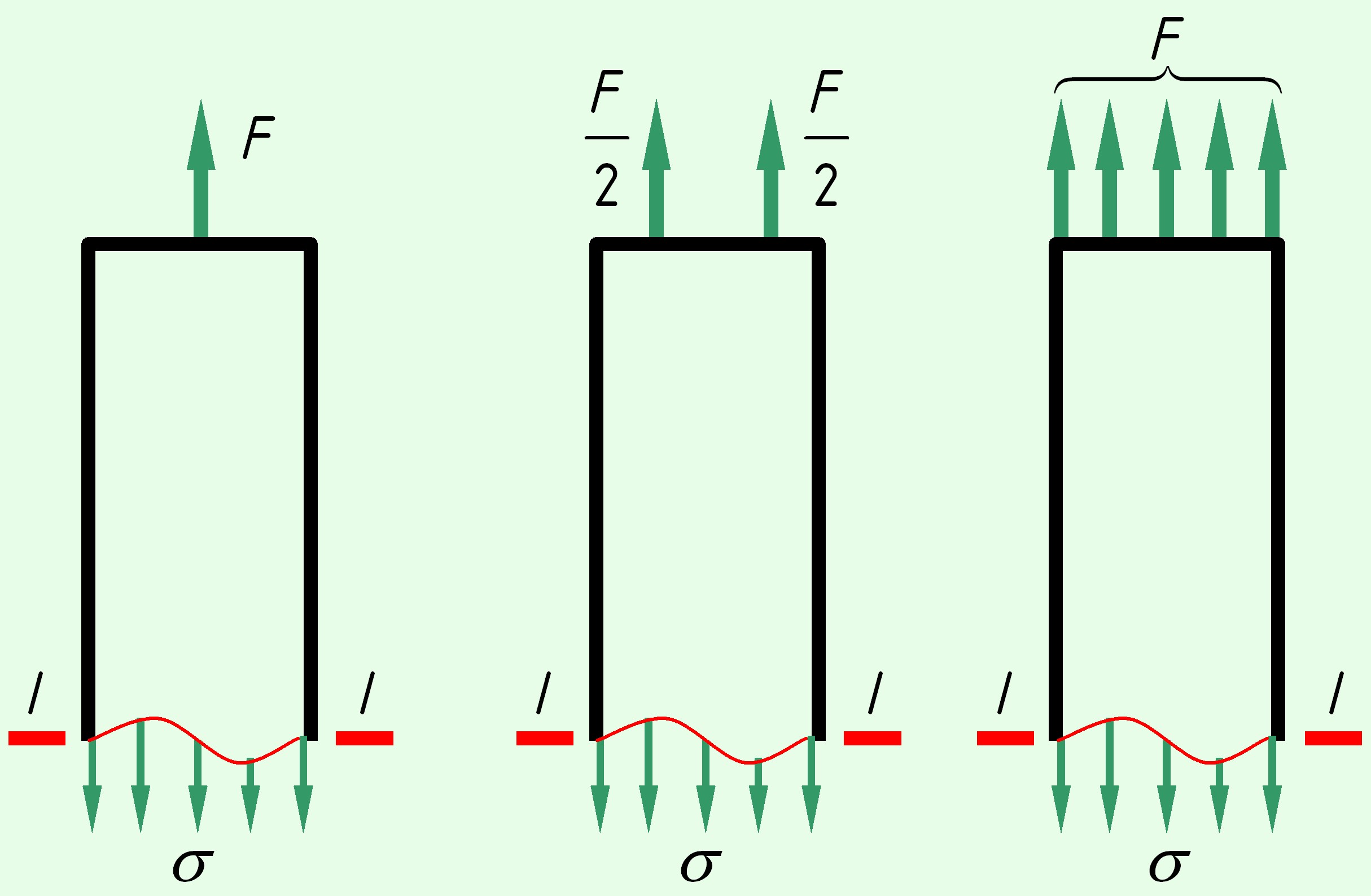
Рисунок - иллюстрация принципа Сен-Венана

Абсолютная и относительная деформация

При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией.

$\Delta l = {l_1} - l$

Относительная деформация – отношение абсолютной деформации к первоначальной длине.

$\varepsilon  = \frac{{\Delta l}}{l}$

$\sigma  = E \cdot \varepsilon $

Таблица - физико-механические характеристики материалов