Кручение

Кручение — это такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор— крутящий момент М.

Деформация кручения возникает при нагрузке стержня парами сил, плоскости действия которых перпендикулярны к его продольной оси.

На рис. а изображен брус, работающий на кручение под действием приложенных к нему крутящих моментов. Это условное изображение моментов равнозначно показанном на рис. б.

Обозначения крутящих моментов

Опыты показывают, что:

соблюдается гипотеза плоских сечений;
сечения при кручении не деформируются;
расстояния между поперечными сечениями не изменяются;
ось стержня остается прямой (не сгибается);
деформация кручения вала эт’связана с деформацией сдвига.

Применяя метод сечений и рассматривая равновесие отсеченной части, приходим к выводу, что внутренние силы, возникающие в поперечном сечении бруса, должны приводиться к крутящего момента, что уравновешивает внешние моменты, приложенные к отсеченной части.

Итак, крутящий момент, возникающий в произвольном поперечном сечении бруса численно равен алгебраической сумме крутящих моментов, приложенных к отсеченной части.

Представление о характере деформации можно получить, подвергая скручиванию резиновую модель бруса с нанесенной на ее поверхности сеткой продольных и поперечных рисок (рис а). Поперечные черточки не искривляются, и расстояния между ними не изменяются, что можно рассматривать как подтверждение первого и второго допущений. Продольные риски обращаются в винтовые линии (рис. б).

Деформации кручения

Справедливость принятых допущений подтверждается, кроме того, и тем, что полученные на основе их формулы совпадают с формулами, полученными в теории упругости без этих допущений, хорошо согласуются с экспериментальными данными.

Рассмотрим брус, жестко защемленный одним концом и нагруженный на свободном конце крутящим моментом . При деформации бруса его поперечные сечения повернутся на некоторые углы относительно своего первоначального положения.

Угол поворота будет тем больше, чем дальше отстоит данный сечения от заделки. Так, для произвольного сечения I, что отстоит от заделки на расстояние , она равна , а для сечения II — . Здесь — угол поворота сечения II относительно I, или угол закручивания элемента бруса длиной .

Вообще угол поворота произвольного сечения равен углу закручивания части бруса, заключенной между этим сечением и заделкой. Таким образом, угол поворота торцевого сечения представляет собой полный угол закручивания рассматриваемого бруса.

Применяя метод сечений, легко убедиться, что крутящий момент во всех поперечных сечениях бруса одинаков: . Выразим его через касательные напряжения, возникающие в поперечном сечении. При этом учтем, что в любой точке поперечного сечения касательное напряжение направлено перпендикулярно к радиусу, проведенному в эту точку (рис. 14.4).

Касательное напряжение

Такое направление напряжений следует из характера деформации: при повороте произвольного поперечного сечения каждая его точка (кроме лежащей на оси бруса) перемещается по дуге окружности, концентричной контура сечения. Другими словами, направление этого перемещения, а значит и возникающего в этой точке касательных напряжений, перпендикулярно соответствующему радиусу.

Направление перемещения и касательных напряжений

Элементарная касательная сила, приходящаяся на площадку , равна , а ее момент относительно оси (точки В):

Суммируя эти элементарные моменты, получаем следующее выражение для крутящего момента:

Хотя крутящий момент может рассматриваться как известная величина (определяется с помощью метода сечений через заданные внешние моменты), использовать выражение для вычисления касательных напряжений невозможно, потому что закон их распределения по поперечному сечении пока неизвестен. Для выяснения этого закона рассмотрим более подробно вопрос о деформации.

Выделим часть бруса двумя бесконечно близкими поперечными сечениями. Будем считать выделенную часть бруса затиснену в сечении I (рис.15.5), что вполне допустимо, потому что нас интересуют ее деформации, а не перемещение в пространстве как твердого тела. Точка В, взята на контуре сечения II, в результате его поворота на угол перейдет в положение Деформация сдвига соответствующего элемента бруса (торец этого элемента, что лежит в сечении II, зачернений) характеризуется углом сдвига Из прямоугольного треугольника , ввиду того, что , и в силу малости деформаций получаем

${\gamma _{\max }} = r \cdot \frac{{d\varphi }}{{d}}$.

Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса, и повторяя те же рассуждения, есть

$\gamma = \rho \cdot \frac{{d\varphi }}{{d}}$.

Применяя закон Гука для сдвига $\left( {\tau = G \cdot \gamma } \right)$, получаем следующее выражение для касательных напряжений

$\tau = G \cdot \rho \cdot \frac{{d\varphi }}{{d}}$.

Подставляя (7.6) в (7.4), получаем

\[{M_z} = \int\limits_A {G \cdot \rho \cdot \frac{{d\varphi }}{{d}} \cdot \rho } \cdot dA\].

При интегрировании по площади поперечного сечения величина постоянная и, так же как и G, может быть вынесена за знак интеграла:

\[{M_z} = G \cdot \frac{{d\varphi }}{{d}} \cdot \int\limits_A {{\rho ^2}} \cdot dA\].

Интеграл, входящий в выражение , представляет собой полярный момент инерции сечения (см. раздел 2), следовательно,

\[{M_z} = G \cdot {I_\rho } \cdot \frac{{d\varphi }}{{d}}\].

откуда

Подставим:

Формула позволяет определить величину касательных напряжений в любой точке поперечного сечения. Из этой формулы следует, что касательные напряжения распределены вдоль любого радиуса сечения по линейному закону.

Эпюры касательных напряжений для круглых сплошных и кольцевого поперечных сечений показаны на рис. 15.6.

Распределение касательных напряжений при кручении

В точках, равноудаленных от центра сечения, напряжения одинаковые. Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения. Они могут быть определены путем подстановки в (7.9) вместо его наибольшего значения, то есть :

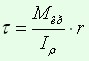Величина $\frac{{{I_\rho }}}{r} = {W_\rho }$ представляет собой полярный момент сопротивления, следовательно, получим следующее выражение для максимального касательных напряжений:

Условие прочности при кручении сплошного круглого вала будет иметь вид

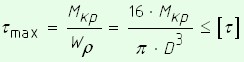Формулу для углов закручивания получим, интегрируя:

\[\varphi = \int\limits_{} {\frac{{{M_z}}}{{G \cdot {I_\rho }}}} \cdot d\].

В частном случае, если диаметр бруса постоянный и крутящий момент во всех сечениях одинаковое значение,

\[\varphi = \frac{{{M_z} \cdot l}}{{G \cdot {I_\rho }}}\].

В случае постоянства крутящего момента лишь в пределах отдельных участков бруса или ступенчатой изменения его поперечного сечения формулу (7.13) можно применять только по участкам.

Произведение $G \cdot {I_\rho }$ называют жесткостью сечения круглого бруса при кручении. Модуль сдвига характеризует свойства материала, а полярный момент инерции является геометрической характеристикой бруса.