Формулы перехода к параллельным осям

Рассмотрим определение моментов инерции плоской фигуры (рис) относительно осей ${Z_1}$ и ${Y_1}$ при известных моментах инерции относительно оси $X$ и $Y$.

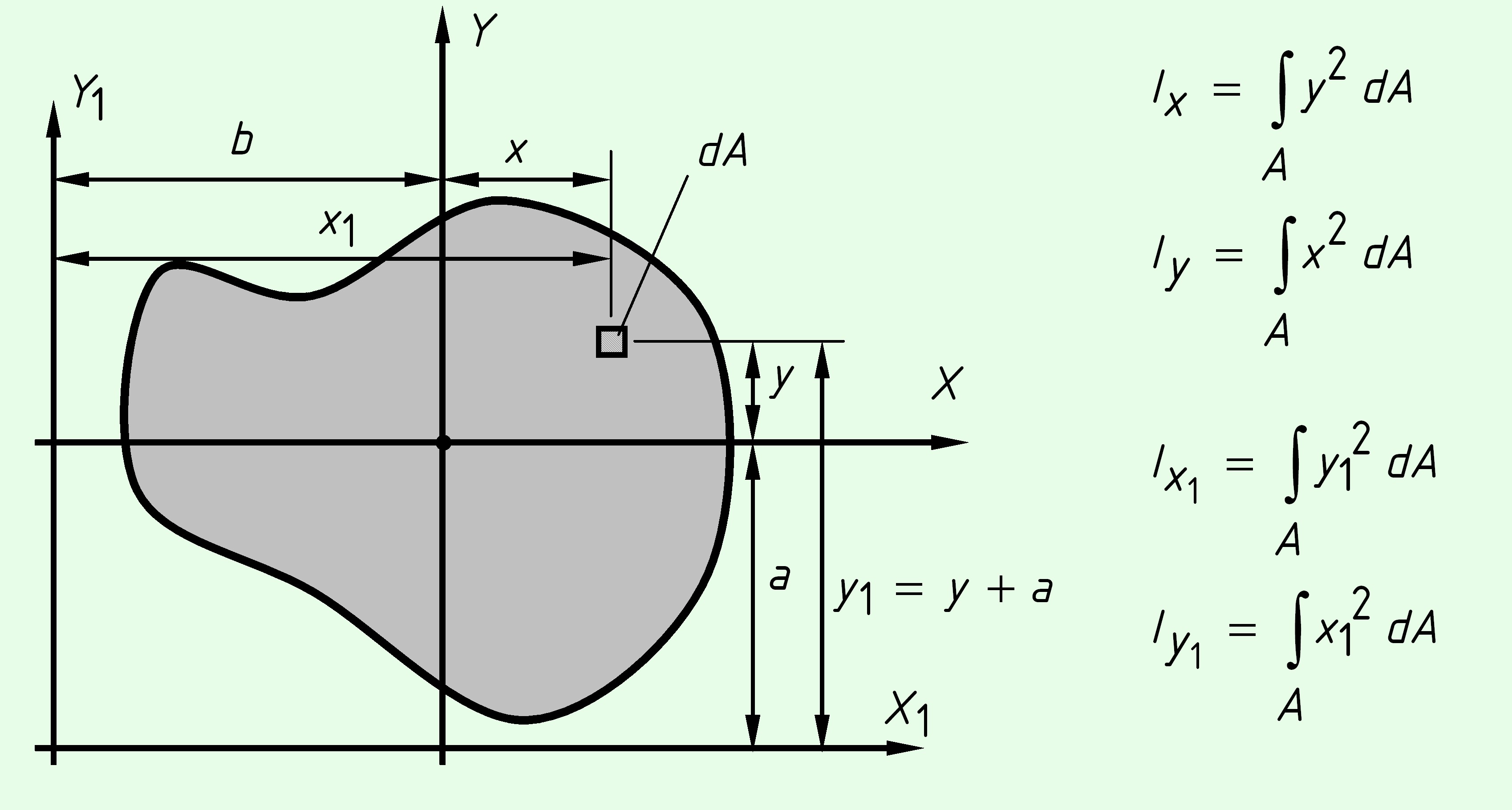
${I_{{x_1}}} = \int\limits_A {y_1^2dA}  = \int\limits_A {{{\left( {y + a} \right)}^2}dA}  = \int\limits_A {\left( {{y^2} + 2ay + {a^2}} \right)dA}  = \int\limits_A {{y^2}dA}  + 2a\int\limits_A {ydA}  + {a^2}\int\limits_A {dA}  = $

$ = {I_x} + 2a{S_x} + {a^2}A$,

где ${S_x}$ – статический момент фигуры относительно оси $X$.

Аналогично относительно оси ${Y_1}$

${I_{{y_1}}} = {I_y} + 2a{S_y} + {b^2}A$.

Центробежный момент инерции относительно осей ${X_1}$ и ${Y_1}$

${I_{{x_1}{y_1}}} = \int\limits_A {{x_1}{y_1}dA}  = \int\limits_A {\left( {x + b} \right)\left( {y + a} \right)dA}  = \int\limits_A {\left( {xy + xa + by + ba} \right)dA}  =  \int\limits_A {xydA}  + a\int\limits_A {xdA}  + b\int\limits_A {ydA}  + ab\int\limits_A {dA}  = {I_{xy}} + a{S_x} + b{S_y} + abA$

Чаще всего используется переход от центральных осей (собственных осей плоской фигуры) в произвольных, параллельных. Тогда ${S_x} = 0$, ${S_y} = 0$, так как оси $X$ и $Y$ являются центральными. Окончательно имеем

где , – собственные моменты инерции, т. е. моменты инерции относительно собственных центральных осей;

$a$, $b$ – расстояния от центральных осей до рассматриваемых;

$A$ – площадь фигуры.

Следует отметить, что при определении центробежного момента инерции в величинах $a$ и $b$ должен быть учтен знак, то есть они являются по сути, координатами центра тяжести фигуры в рассматриваемых осях. При определении осевых моментов инерции эти величины подставляют по модулю (как расстояния), поскольку они все равно возвышаются до квадрата.

С помощью формул параллельного переноса возможно осуществлять переход от центральных осей к произвольным, или же наоборот – от произвольных центральных осей. Первый переход осуществляется со знаком "+". Второй переход осуществляется со знаком "–".

Примеры использования формул перехода между параллельными осями

Прямоугольное сечение

Определим центральные моменты инерции прямоугольника при известных моментах инерции относительно осей $Z$ и $Y$.

${I_x} = \frac{{b{h^3}}}{3}$; ${I_y} = \frac{{h{b^3}}}{3}$.

.

Аналогично ${I_y} = \frac{{h{b^3}}}{{12}}$.

Треугольное сечение

Определим центральные моменты инерции треугольника при известном моменте инерции относительно основы ${I_x} = \frac{{b{h^3}}}{{12}}$.

.

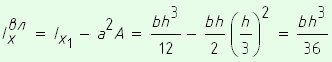Относительно центральной оси ${Y_c}$ треугольник имеет другую конфигурацию, поэтому рассмотрим следующее. Момент инерции всей фигуры относительно оси ${Y_c}$ равен сумме момента инерции треугольника $ABD$ относительно оси ${Y_c}$ и момента инерции треугольника $CBD$ относительно оси ${Y_c}$, то есть

.

Определение момента инерции составного сечения

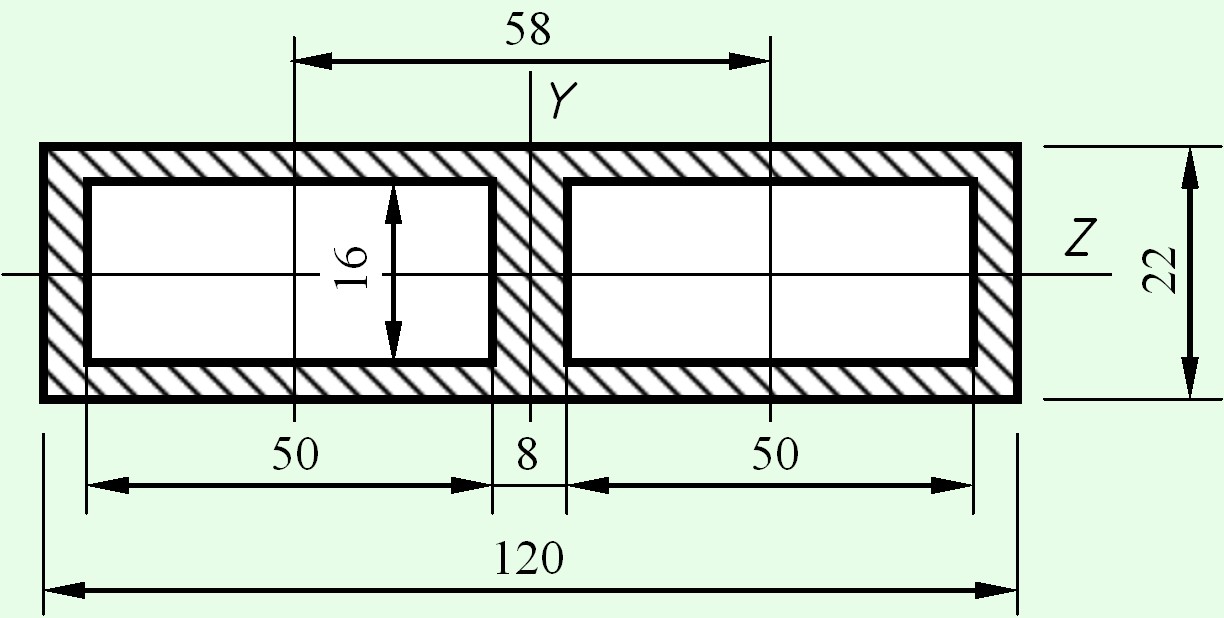
Составленным считаем сечение, состоит из отдельных элементов, геометрические характеристики которых известны. Площадь, статический момент и моменты инерции составной фигуры равны сумме соответствующих характеристик их составляющих. Если составлен сечение можно образовать путем вырезания одной фигуры из другой, геометрические характеристики вырезанной фигуры вычитаются. Например, моменты инерции составной фигуры, показанной на рис. будут определяться так

$I_z^{} = \frac{{120 \cdot {{22}^3}}}{{12}} - 2 \cdot \frac{{50 \cdot {{16}^3}}}{{12}} = 72\,300$см⁴.

$I_y^{} = \frac{{22 \cdot {{120}^3}}}{{12}} - 2 \cdot \left( {\frac{{16 \cdot {{50}^3}}}{{12}} + 50 \cdot 16 \cdot {{29}^2}} \right) = 1\,490\,000$см⁴