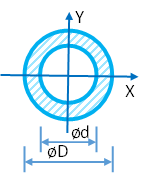
Внешний диаметр D =
Внутренний диаметр d =
Ответ: $A = 126$, $J_x = 6350$, $J_{\rho} = 12700$, $W_x = 577$, $W_{\rho} = 1155$
А теперь поподробнее:
Площадь сечения $$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot (22^2-18^2)}{4} = 126$$
Отношение диаметров $$\alpha = \frac{ d }{ D } = \frac{ 18 }{ 22 } = 0.818$$
Осевые моменты инерции кольцевого (трубчатого) сечения $$J_x = J_y = \frac{\pi \cdot D^4}{64}(1-\alpha^4) = \frac{\pi \cdot 22^4}{64}(1-0.818^4) = 6350$$
Осевые моменты сопротивления $$W_x = W_y = \frac{\pi \cdot D^3}{32}(1-\alpha^4) = \frac{\pi \cdot 22^3}{32}(1-0.818^4) = 577$$
Полярный момент инерции $$J_{\rho} = \frac{\pi \cdot d^4}{32}(1-\alpha^4) = \frac{\pi \cdot 22^4}{32}(1-0.818^4) = 12700$$
Полярный момент сопротивления $$W_{\rho} = \frac{\pi \cdot d^3}{16}(1-\alpha^4) = \frac{\pi \cdot 22^3}{16}(1-0.818^4) = 1155$$
