Максимальный момент в балке Mmax =
кНм
Допускаемые напряжения [σ] =
МПа
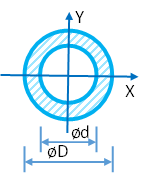
Отношение внутреннего диаметра к внешнему $ \alpha = \frac{ d}{ D} $ =
Необходимый минимальный момент сопротивления равен $$W = \frac{M_{max}}{[\sigma]} = \frac{5000}{160} = 31.3см^3$$
Поскольку момент сопротивления кольца (трубы) $$W=\frac{\pi \cdot D^3}{32}(1-\alpha^4)$$ наружный диаметр сечения балки равен $$D = \sqrt[3]{\frac{32\cdot W}{\pi (1-\alpha^4)}} = \sqrt[3]{\frac{32\cdot 31.3}{\pi (1-0.9^4)}} = 9.75 см$$ Внутренний диаметр $$d=9.75\cdot 0.9 = 8.78 см$$ Площадь сечения балки $$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 9.75^2}{4}- \frac{\pi \cdot 8.78^2}{4} = 14.1см^2$$
Поскольку момент сопротивления кольца (трубы) $$W=\frac{\pi \cdot D^3}{32}(1-\alpha^4)$$ наружный диаметр сечения балки равен $$D = \sqrt[3]{\frac{32\cdot W}{\pi (1-\alpha^4)}} = \sqrt[3]{\frac{32\cdot 31.3}{\pi (1-0.9^4)}} = 9.75 см$$ Внутренний диаметр $$d=9.75\cdot 0.9 = 8.78 см$$ Площадь сечения балки $$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 9.75^2}{4}- \frac{\pi \cdot 8.78^2}{4} = 14.1см^2$$
