Максимальный момент в балке Mmax = кНм
Допускаемые напряжения [σ] = МПа
Отношение высоты к ширине h / b =
Необходимый минимальный момент сопротивления равен
$$W = \frac{M_{max}}{[\sigma]} = \frac{45000}{160} = 281см^3$$
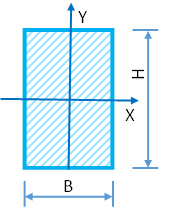
Момент сопротивления прямоугольника $$W=\frac{b \cdot h^2}{6} = \frac{b \cdot (2.5b)^2}{6} = \frac{b^3 \cdot 2.5^2}{6}$$ ширина сечения балки $$b = \sqrt[3]{\frac{6\cdot W}{{hb}^2}} = \sqrt[3]{\frac{6\cdot 281}{2.5^2}} = 6.46 см$$ Высота сечения $$h=6.46\cdot 2.5 = 16.2 см$$ Площадь сечения балки $$A = h \cdot b = 16.2\cdot 6.46 = 105см^2$$
Момент сопротивления прямоугольника $$W=\frac{b \cdot h^2}{6} = \frac{b \cdot (2.5b)^2}{6} = \frac{b^3 \cdot 2.5^2}{6}$$ ширина сечения балки $$b = \sqrt[3]{\frac{6\cdot W}{{hb}^2}} = \sqrt[3]{\frac{6\cdot 281}{2.5^2}} = 6.46 см$$ Высота сечения $$h=6.46\cdot 2.5 = 16.2 см$$ Площадь сечения балки $$A = h \cdot b = 16.2\cdot 6.46 = 105см^2$$
