Моменты инерции и моменты сопротивления применяются при расчете прочности и деформаций в стержнях, балках, валах и т.д.
Их значения могут быть вычислены: для простых фигур (круг, прямоугольник и т.д.) - по формулам, для стандартных профилей - по специальным таблицам ГОСТов (так называемые сортаменты ).
Здесь собраны онлайн-калькуляторы площади, моментов инерции и моментов сопротивления простых фигур.
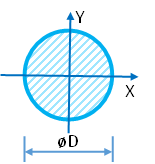
Момент инерции круга
Диаметр d = Рассчитать
Площадь круга
$$A = \frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 22^2}{4} = 380$$
Осевые моменты инерции круга
$$J_x = J_y = \frac{\pi \cdot d^4}{64} = \frac{\pi \cdot 22^4}{64} = 11500$$
Осевые моменты сопротивления круга
$$W_x = W_y = \frac{\pi \cdot d^3}{32} = \frac{\pi \cdot 22^3}{32} = 1045$$
Полярный момент инерции круга
$$J_{\rho} = \frac{\pi \cdot d^4}{32} = \frac{\pi \cdot 22^4}{32} = 23000$$
Полярный момент сопротивления круга
$$W_{\rho} = \frac{\pi \cdot d^3}{16} = \frac{\pi \cdot 22^3}{16} = 2091$$
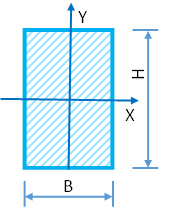
Моменты инерции прямоугольника
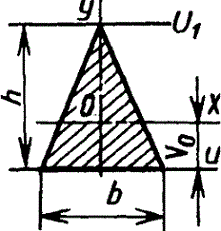
Моменты инерции треугольника равнобедренного
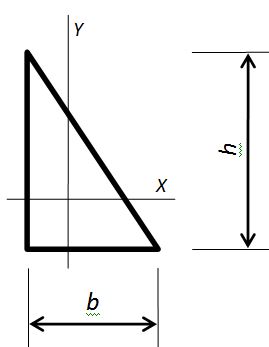
Моменты инерции треугольника прямоугольного
Ширина b = Рассчитать
Площадь прямоугольника
$$A = \frac{b \cdot h}{2} = \frac{ 20 \cdot 36 }{2} = 360$$
Осевые моменты инерции
$$J_x = \frac{b \cdot h^3}{36} = \frac{ 20 \cdot 36^3 }{36} = 25920$$
$$J_y = \frac{b^3 \cdot h}{48} = \frac{ 20^3 \cdot 36 }{36} = 8000$$
Центробежный момент инерции
$$J_{xy} = \frac{b^2 \cdot h^2}{72} = \frac{ 20^2 \cdot 36^2 }{72} = 7200$$
Осевые моменты сопротивления
$$W_x = \frac{b \cdot h^2}{24} = \frac{ 20\cdot 36^2 }{24} = 1080$$
$$W_y = \frac{b^2 \cdot h}{24} = \frac{ 20^2 \cdot 36 }{24} = 600$$
Для составных сечений моменты инерции определяются как сумма (разница) моментов инерции составных частей.
Момент инерции кольцевого сечения
Внешний диаметр D = Рассчитать
Ответ: $A = 126$, $J_x = 6350$, $J_{\rho} = 12700$, $W_x = 577$, $W_{\rho} = 1155$
А теперь поподробнее:
Площадь сечения
$$A = \frac{\pi \cdot D^2}{4}-\frac{\pi \cdot d^2}{4} = \frac{\pi \cdot (22^2-18^2)}{4} = 126$$
Отношение диаметров
$$\alpha = \frac{ d }{ D } = \frac{ 18 }{ 22 } = 0.818$$
Осевые моменты инерции кольцевого (трубчатого) сечения
$$J_x = J_y = \frac{\pi \cdot D^4}{64}(1-\alpha^4) = \frac{\pi \cdot 22^4}{64}(1-0.818^4) = 6350$$
Осевые моменты сопротивления
$$W_x = W_y = \frac{\pi \cdot D^3}{32}(1-\alpha^4) = \frac{\pi \cdot 22^3}{32}(1-0.818^4) = 577$$
Полярный момент инерции
$$J_{\rho} = \frac{\pi \cdot d^4}{32}(1-\alpha^4) = \frac{\pi \cdot 22^4}{32}(1-0.818^4) = 12700$$
Полярный момент сопротивления
$$W_{\rho} = \frac{\pi \cdot d^3}{16}(1-\alpha^4) = \frac{\pi \cdot 22^3}{16}(1-0.818^4) = 1155$$