Расчет балки

Подробный ход решения - расчет балки, построение эпюр

Составим уравнения равновесия для определения реакций опор

Равнодействующая распределенной нагрузки q равна Q1 = q · 3 = 8· 3 = 24кН

Σ M_B = + Q1 · 0.5 + M + P · 2 - R_D · 5= + 24 · 0.5 + 14 + 12 · 2 - R_D · 5=0

Σ M_D = - Q1 · 4.5 + M - P · 3 + R_B · 5= - 24 · 4.5 + 14 - 12 · 3 + R_B · 5=0

Из этих уравнений находим реакции опор

R_B = 26кН.

R_D = 10кН.

Проверка

Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 1 м )

Q(z₁) = - q·z = - 8·z

Q(0) = 0 кН

Q(1) = -8 кН

M(z₁) = - q·z²/2 + M = - 8·z²/2 + 14

M(0) = 14 кНм

M(1) = 10 кНм

Поскольку поперечная сила на участке пересекает ноль при z = 0 м, в этой точке будет экстремум на эпюре M

M(0) = 14 кНм

На участке BC: (1 ≤ z₂ ≤ 3 м )

Q(z₂) = + R_B - q·z = + 26 - 8·z

Q(1) = 18 кН

Q(3) = 2 кН

M(z₂) = + R_B · (z - 1) - q·z²/2 + M = + 26 · (z - 1) - 8·z²/2 + 14

M(1) = 10 кНм

M(3) = 30 кНм

На участке CD: (3 ≤ z₃ ≤ 6 м )

Q(z₃) = + R_B - Q₁ - P = + 26 - 24 - 12 = -10 кН

M(z₃) = + R_B · (z - 1) - Q₁·(z - 1.5) + M - P·(z - 3) = + 26 · (z - 1) - 24·(z - 1.5) + 14 - 12·(z - 3)

M(3) = 30 кНм

M(6) = -0 кНм

Максимальный момент в балке составляет M_max = 30 кНм. По этому значению подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Подбираем двутавровое сечение при допускаемом напряжении [σ] = 160 МПа
W_min=30000 / 160 = 187.5 см³
Из сортамента выбираем двутавр №22 с моментом сопротивления W = 231.82 см³ и площадью A = 30.6 см²
Максимальные нормальные напряжения в двутавре составляют
σ_max = M_max/Wx = 30000/231.82 = 129.41 МПа
Максимальные касательные напряжения в двутавре (на центральной оси) составляют
τ_max = Q_max×Sx/b×Ix = 18000×114.96×10^-6/0.0054×2550×10^-8 = 15.027×10⁶ Па = 15.027 МПа
Касательные напряжения на границе полки и стенки составляют
τ_max = Q_max×Sx'/b×Ix = 18000×101.11×10^-6/0.0054×2550×10^-8 = 13.217×10⁶ Па = 13.217 МПа,
где статический момент отсеченной полки составляет
Sx'=b×t×(h-t)/2=11×0.87×(22-0.87)/2=101.11 см³.
Эпюры нормальных и касательных напряжений для двутавра:

Подбираем круг.
W_min=30000/20=1500 см³
Момент сопротивления сплошного круглого сечения
W=π×d³ / 32
d³=32×W / π = 32×1500 / π = 15287
Диаметр сечения будет таким d=24.8 см
Площадь сечения
A=π×d²/4=π×24.8²/4=482.81 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×d³ = 32×30000/π×24.8³ = 20.04 МПа
Максимальные касательные напряжения для круга составляют
τ_max = 4Q_max/3A = 4×18000/3×482.81×100 = 0.497 МПа
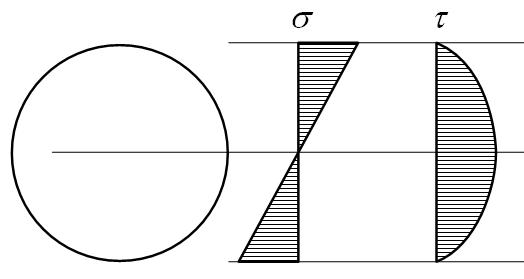
Эпюры нормальных и касательных напряжений для круга:

Подбираем трубу с отношением диаметров α = d/D = 0.9
W_min=30000 / 20=1500 см³
Момент сопротивления трубчатого сечения
W=π×D³ ×(1-α⁴)/32
D³=32×W / π×(1-α⁴) = 32×1500 / π×(1-0.9⁴)=44451
Диаметр сечения будет таким D=35.4 см
Площадь сечения A=π×D²(1-α²)/4=π×35.4²(1-0.9²)/4=186.91 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×D³×(1-α⁴) = 32×30000/π×35.4³×(1-0.9⁴) = 20.04 МПа
Максимальные касательные напряжения для трубы определим по формуле Журавского
τ_max = Q_max×Sx/b×Ix, где b=D-d
Статический момент полусечения
Sx=2R³/3-2r³/3=(D³-d³)/12=(35.4³-(35.4×0.9)³)/12=1001.84 см³
Момент инерции сечения
Ix=π×D⁴×(1-α⁴)/64=π×35.4⁴×(1-0.9⁴)/64=26496.89 см⁴
τ_max = 18000×1001.84×10^-6/(35.4-0.9×35.4)×0.01×26496.89^-8=0.019×10⁶ Па = 0.019 МПа
Эпюры нормальных и касательных напряжений для трубы:

Подбираем квадрат.
W_min=30000 / 20=1500 см³
Момент сопротивления квадратного сечения
W=a³/6
Сторона квадрата будет такой a= 20.8 см
Площадь сечения A=a²=20.8²=432.64 см²

Подбираем прямоугольное сечение с отношением сторон h / b=2.5
W_min=30000 / 20 = 1500 см³
Момент сопротивления прямоугольного сечения
W=b×h² / 6 = b³ × 2.5² / 6 = b³×1.04
b³=1500 / 1.04=1442
Ширина сечения b=11.3 см, Высота сечения h=b×2.5=11.3×2.5=28.25 см
Площадь сечения A=b×h=11.3×28.25=319.225 см²
Максимальные нормальные напряжения составляют
σ_max = 6×M_max/b×h² = 6×30000/11.3×28.25² = 19.96 МПа
Максимальные касательные напряжения для прямоугольника составляют
τ_max = 3Q_max/2A = 3×18000/2×319.225×100 = 0.846 МПа
Эпюры нормальных и касательных напряжений для прямоугольного сечения:

Определяем прогибы и углы поворота сечений с помощью метода начальных параметров

Участок AB: (0 ≤ z₁ ≤ 1 м )

EJ×φ(z) = EJ×φ₀ - q·z³/6 + M· z

EJ×v(z) = EJ×v₀ + EJ×φ₀×z - q·z⁴/24 + M· z²/2

Участок BC: (1 ≤ z₂ ≤ 3 м )

EJ×φ(z) = EJ×φ₀ + R_B·(z - 1)²/2 - q·z³/6 + M· z

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_B·(z - 1)³/6 - q·z⁴/24 + M· z²/2

Участок CD: (3 ≤ z₃ ≤ 6 м )

EJ×φ(z) = EJ×φ₀ + R_B·(z - 1)²/2 - q₁·z³/6 + q₁·(z - 3)³/6 + M· z - P·(z - 3)²/2

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_B·(z - 1)³/6 - q₁·z⁴/24 + q₁·(z - 3)⁴/24 + M· z²/2 - P·(z - 3)³/6

Начальный прогиб и начальный угол поворота определяем по условиям закрепления балки:

- начальный угол поворота EJ·φ₀ = -65.6 кНм²

- начальный прогиб EJ·v₀ = 58.93 кНм³

Углы поворота и прогибы сечений

Участок AB

EJ×φ(0) = -65.6 кНм²

EJ×v(0) = 58.93 кНм³

EJ×φ(0.25) = -62.12 кНм²

EJ×v(0.25) = 42.97 кНм³

EJ×φ(0.5) = -58.77 кНм²

EJ×v(0.5) = 27.86 кНм³

EJ×φ(0.75) = -55.66 кНм²

EJ×v(0.75) = 13.57 кНм³

EJ×φ(1) = -52.93 кНм²

EJ×v(1) = 0 кНм³

Участок BC

EJ×φ(1) = -52.93 кНм²

EJ×v(1) = 0 кНм³

EJ×φ(1.5) = -45.85 кНм²

EJ×v(1.5) = -24.86 кНм³

EJ×φ(2) = -35.27 кНм²

EJ×v(2) = -45.27 кНм³

EJ×φ(2.5) = -22.18 кНм²

EJ×v(2.5) = -59.71 кНм³

EJ×φ(3) = -7.6 кНм²

EJ×v(3) = -67.2 кНм³

Участок CD

EJ×φ(3) = -7.6 кНм²

EJ×v(3) = -67.2 кНм³

EJ×φ(3.75) = 12.09 кНм²

EJ×v(3.75) = -65.17 кНм³

EJ×φ(4.5) = 26.15 кНм²

EJ×v(4.5) = -50.48 кНм³

EJ×φ(5.25) = 34.59 кНм²

EJ×v(5.25) = -27.35 кНм³

EJ×φ(6) = 37.4 кНм²

EJ×v(6) = 0 кНм³