Моменты инерции
Осевым моментом инерции площади сечения относительно оси, рассматривается, называется сумма (интеграл), который рассчитывается по всей площади сечения от произведения площади элементарной площадки на квадрат расстояния до оси, что рассматривается.
${I_x} = \int\limits_A {{y^2}dA} $; ${I_y} = \int\limits_A {{x^2}dA} $ (см4)
Осевые моменты ${I_x}$ и ${I_y}$ всегда больше нуля, поскольку координата $x$ или $y$ возвышается до квадрата.
Примеры определения осевых моментов инерции
Прямоугольное сечение
Для интегрирования выделим элементарную площадь в виде полосы $b \cdot dy$, для которой координата $y$ стала.

Треугольное сечение

Для определения момента инерции относительно оси $X$ выбираем элементарную полоску длиной $b(y)$ и высотой $dy$. Тогда площадь элементарной полоски будет равна: $dA = b(y)dy$.
Из подобия двух треугольников можем записать:
$\frac{{b(y)}}{b} = \frac{{h - y}}{h} \Rightarrow b(y) = \frac{b}{h}\left( {h - y} \right) \Rightarrow $
$ \Rightarrow {I_x} = \int\limits_A {{y^2}dA} = \frac{b}{h}\int\limits_0^h {\left( {h - y} \right){y^2}dy} = \frac{b}{h}\left. {\left( {h\frac{{{y^3}}}{3} - \frac{{{y^4}}}{4}} \right)} \right|_0^h = $$\frac{{b{h^3}}}{{12}}$.
Проводя ось $OX$ через основание треугольника мы не накладывали на его форму никаких условий. Таким образом, момент инерции любого треугольника относительно оси, приходящей через его основу будет равна $\frac{{b{h^3}}}{{12}}$.
Полярным моментом инерции площади сечения относительно данной точки (полюса) называется интеграл по всей площади сечения от произведения площади элементарной площадки на квадрат расстояния до полюса.
${I_\rho } = \int\limits_A {{\rho ^2}dA} = \int\limits_A {\left( {{x^2} + {y^2}} \right)dA} = \int\limits_A {{x^2}dA} + \int\limits_A {{y^2}dA} = {I_z} + {I_y}$,
где ${\rho ^2} = {y^2} + {z^2}$
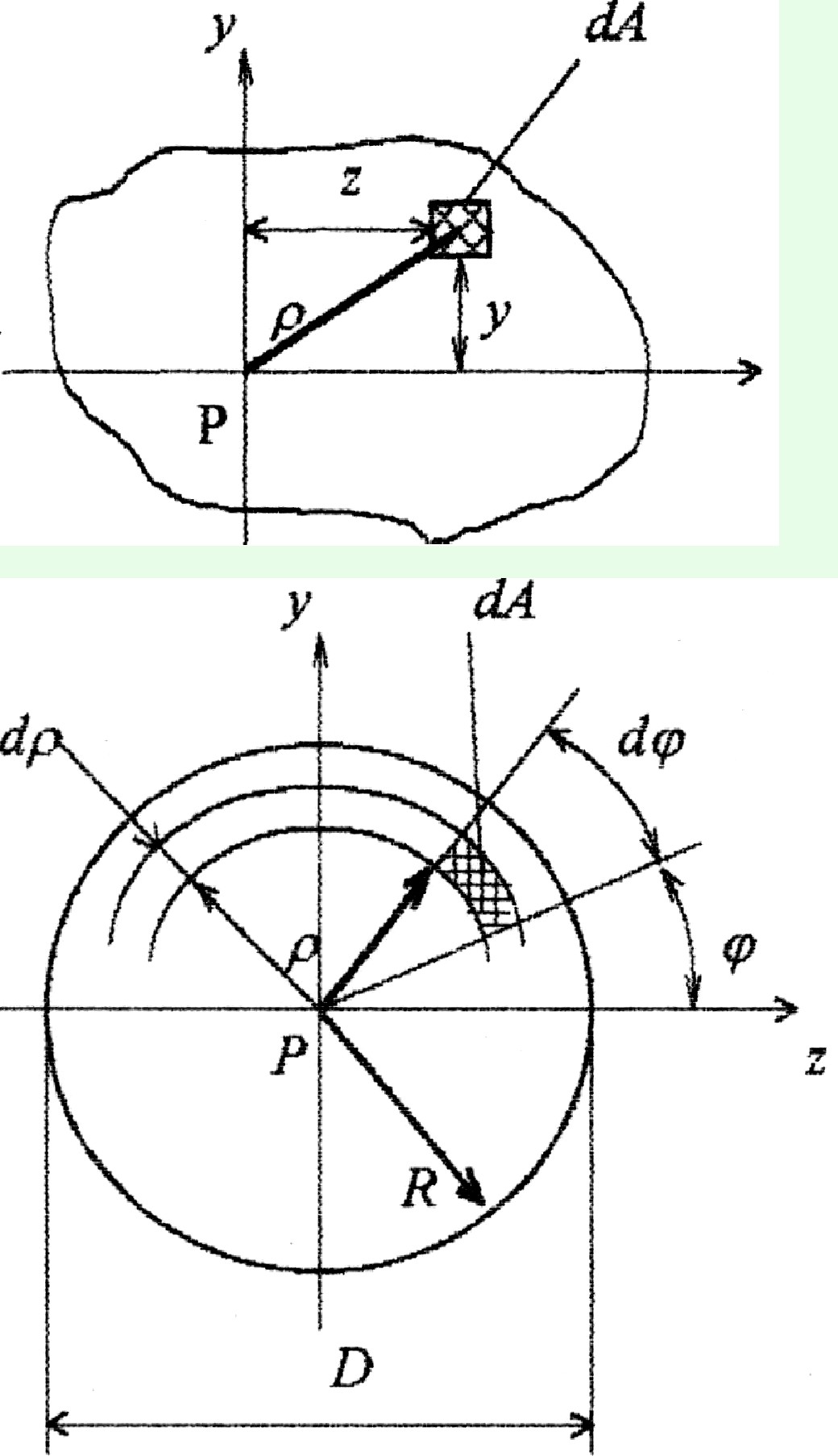
Другими словами: полярный момент инерции площади сечения относительно точки пересечения двух перпендикулярных осей (полюса) равна сумме осевых моментов инерции.
Пример
Определить величину ${I_\rho }$ круга:
$dA = \rho d\rho d\varphi $
$\begin{gathered} {I_\rho } = \int\limits_A {{\rho ^2}dA} = \int\limits_0^{2\pi } {\left( {\int\limits_0^R {{\rho ^3}d\rho } } \right)d\varphi } = \int\limits_0^R {{\rho ^3}d\rho \int\limits_0^{2\pi } {d\varphi } } = \frac{{\pi {R^4}}}{2} = \frac{{\pi {D^4}}}{{32}}. \hfill \\ \end{gathered} $
${I_\rho } = \frac{{\pi {D^4}}}{{32}}$$ \Rightarrow $${I_z} = {I_y} = \frac{1}{2}{I_\rho } = \frac{{\pi {D^4}}}{{64}}$.
Центробежным моментом инерции площади сечения относительно двух взаимно перпендикулярных осей называется интеграл по площади сечения от произведения площади элементарной площадки на расстоянии от центра тяжести этой площадки до соответствующих осей.
${I_{xy}} = \int\limits_A {yxdA} $ (см4)
Основные особенности центробежного момента инерции.
1. Основной особенностью ${I_{xy}}$ является то, что он может быть положительным, отрицательным и равняться нулю.
2. Оси, относительно которых центробежный момент инерции равен нулю, носят название главных осей инерции.
3. Оси, проходящие через центр тяжести сечения, или, другими словами, в отношении которых одновременно центробежный момент инерции и статический момент площади сечения равны нулю, называются главными центральными осями инерции.
4. Главными центральными моментами инерции площади сечения называются моменты инерции относительно главных центральных осей.
5. Теорема:

5.1. Если сечение, рассматривается, имеет три и более осей симметрии, то любая центральная ось этого сечения является главной.
5.2. Центробежный момент инерции площади сечения рассчитывается относительно двух взаимно перпендикулярных осей, из которых одна является осью симметрии, будет равняться нулю.
Пример: $h$, $b$, $\angle ABC = {90^ \circ }$ Найти: ${I_{xy}}$
${I_{xy}} = \int\limits_0^b {\int\limits_0^{\left( {h - \frac{h}{b}z} \right)} {xydy} dx} = \int\limits_0^b {\left( {\int\limits_0^{\left( {h - \frac{h}{b}z} \right)} {ydy} } \right)xdx} = $
$ = \int\limits_0^b {\left( {\left. {\left( {\frac{{{y^2}}}{2}} \right)} \right|_0^{\left( {h - \frac{h}{b}x} \right)}} \right)xdx} = \frac{1}{2}\left. {\left( {\frac{{{h^2}{x^2}}}{2} - \frac{{2{h^2}}}{b} \cdot \frac{{{x^3}}}{3} + \frac{{{h^2}{x^4}}}{{4{b^2}}}} \right)} \right|_0^b = \frac{{{b^2}{h^2}}}{{24}}$.
\[{I_{xy}} = \frac{{{b^2}{h^2}}}{{24}}\].