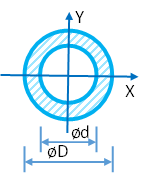
Диаметр d =
Площадь круга $$A = \frac{\pi \cdot d^2}{4} = \frac{\pi \cdot 22^2}{4} = 380$$
Осевые моменты инерции круга $$J_x = J_y = \frac{\pi \cdot d^4}{64} = \frac{\pi \cdot 22^4}{64} = 11500$$
Осевые моменты сопротивления круга $$W_x = W_y = \frac{\pi \cdot d^3}{32} = \frac{\pi \cdot 22^3}{32} = 1045$$
Полярный момент инерции круга $$J_{\rho} = \frac{\pi \cdot d^4}{32} = \frac{\pi \cdot 22^4}{32} = 23000$$
Полярный момент сопротивления круга $$W_{\rho} = \frac{\pi \cdot d^3}{16} = \frac{\pi \cdot 22^3}{16} = 2091$$