Расчет балки

Подробный ход решения - расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 16·2 = 32кН

Составим уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + Q1 · 3 - M - R_E · 6= + 412 · 2 + 32 · 3 - 10 - R_E · 6=0

Σ M_E = - P · 4 - Q1 · 3 - M + R_A · 6= - 412 · 4 - 32 · 3 - 10 + R_A · 6=0

Из этих уравнений находим реакции опор

R_A = 292.3кН.

R_E = 151.7кН.

Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 292.3 = 292.333 кН

M(z₁) = + R_A · z = + 292.3 · z

M(0) = -0 кНм

M(2) = 584.667 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A - P - q₁·(z - 2) = + 292.3 - 412 - 16·(z - 2)

Q(2) = -119.667 кН

Q(4) = -151.667 кН

M(z₂) = + R_A · z - P·(z - 2) - q₁·(z - 2)²/2 = + 292.3 · z - 412·(z - 2) - 16·(z - 2)²/2

M(2) = 584.667 кНм

M(4) = 313.333 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A - P - Q₁ = + 292.3 - 412 - 32 = -151.667 кН

M(z₃) = + R_A · z - P·(z - 2) - Q₁·(z - 3) = + 292.3 · z - 412·(z - 2) - 32·(z - 3)

M(4) = 313.333 кНм

M(5) = 161.667 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A - P - Q₁ = + 292.3 - 412 - 32 = -151.667 кН

M(z₄) = + R_A · z - P·(z - 2) - Q₁·(z - 3) - M = + 292.3 · z - 412·(z - 2) - 32·(z - 3) - 10

M(5) = 151.667 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 585 кНм. По этому значению подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Подбираем двутавровое сечение при допускаемом напряжении [σ] = 160 МПа
W_min=585000 / 160 = 3656.25 см³
Из сортамента выбираем двутавр № с моментом сопротивления W = NAN см³ и площадью A = см²
Максимальные нормальные напряжения в двутавре составляют
σ_max = M_max/Wx = 585000/NAN = NAN МПа
Максимальные касательные напряжения в двутавре (на центральной оси) составляют
τ_max = Q_max×Sx/b×Ix = 292000×0×10^-6/0××10^-8 = NAN×10⁶ Па = NAN МПа
Касательные напряжения на границе полки и стенки составляют
τ_max = Q_max×Sx'/b×Ix = 292000×0×10^-6/0××10^-8 = NAN×10⁶ Па = NAN МПа,
где статический момент отсеченной полки составляет
Sx'=b×t×(h-t)/2=0×0×(0-0)/2=0 см³.
Эпюры нормальных и касательных напряжений для двутавра:

Подбираем круг.
W_min=585000/160=3656 см³
Момент сопротивления сплошного круглого сечения
W=π×d³ / 32
d³=32×W / π = 32×3656 / π = 37259
Диаметр сечения будет таким d=33.4 см
Площадь сечения
A=π×d²/4=π×33.4²/4=875.71 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×d³ = 32×585000/π×33.4³ = 160.01 МПа
Максимальные касательные напряжения для круга составляют
τ_max = 4Q_max/3A = 4×292000/3×875.71×100 = 4.446 МПа
Эпюры нормальных и касательных напряжений для круга:

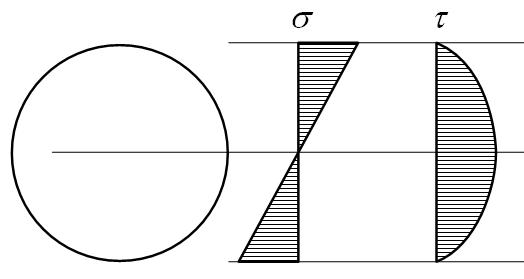
Подбираем трубу с отношением диаметров α = d/D = 0.9
W_min=585000 / 160=3656 см³
Момент сопротивления трубчатого сечения
W=π×D³ ×(1-α⁴)/32
D³=32×W / π×(1-α⁴) = 32×3656 / π×(1-0.9⁴)=108341
Диаметр сечения будет таким D=47.7 см
Площадь сечения A=π×D²(1-α²)/4=π×47.7²(1-0.9²)/4=339.36 см²
Максимальные нормальные напряжения составляют
σ_max = 32×M_max/π×D³×(1-α⁴) = 32×585000/π×47.7³×(1-0.9⁴) = 159.73 МПа
Максимальные касательные напряжения для трубы определим по формуле Журавского
τ_max = Q_max×Sx/b×Ix, где b=D-d
Статический момент полусечения
Sx=2R³/3-2r³/3=(D³-d³)/12=(47.7³-(47.7×0.9)³)/12=2451 см³
Момент инерции сечения
Ix=π×D⁴×(1-α⁴)/64=π×47.7⁴×(1-0.9⁴)/64=87348.48 см⁴
τ_max = 292000×2451×10^-6/(47.7-0.9×47.7)×0.01×87348.48^-8=0.172×10⁶ Па = 0.172 МПа
Эпюры нормальных и касательных напряжений для трубы:

Подбираем квадрат.
W_min=585000 / 160=3656 см³
Момент сопротивления квадратного сечения
W=a³/6
Сторона квадрата будет такой a= 28 см
Площадь сечения A=a²=28²=784 см²

Подбираем прямоугольное сечение с отношением сторон h / b=2
W_min=585000 / 160 = 3656 см³
Момент сопротивления прямоугольного сечения
W=b×h² / 6 = b³ × 2² / 6 = b³×0.67
b³=3656 / 0.67=5457
Ширина сечения b=17.6 см, Высота сечения h=b×2=17.6×2=35.2 см
Площадь сечения A=b×h=17.6×35.2=619.52 см²
Максимальные нормальные напряжения составляют
σ_max = 6×M_max/b×h² = 6×585000/17.6×35.2² = 160.96 МПа
Максимальные касательные напряжения для прямоугольника составляют
τ_max = 3Q_max/2A = 3×292000/2×619.52×100 = 7.07 МПа
Эпюры нормальных и касательных напряжений для прямоугольного сечения:

Записываем уравнения углов поворота и прогибов по методу начальных параметров

На участке AB: (0 ≤ z₁ ≤ 2 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6

На участке BC: (2 ≤ z₂ ≤ 4 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 - P·(z - 2)²/2 - q₁·(z - 2)³/6

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 - P·(z - 2)³/6 - q₁·(z - 2)⁴/24

На участке CD: (4 ≤ z₃ ≤ 5 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 - P·(z - 2)²/2 - q₁·(z - 2)³/6 + q₁·(z - 4)³/6

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 - P·(z - 2)³/6 - q₁·(z - 2)⁴/24 + q₁·(z - 4)⁴/24

На участке DE: (5 ≤ z₄ ≤ 6 м )

EJ×φ(z) = EJ×φ₀ + R_A·z²/2 - P·(z - 2)²/2 - q₁·(z - 2)³/6 + q₁·(z - 4)³/6 - M· (z - 5)

EJ×v(z) = EJ×v₀ + EJ×φ₀×z + R_A·z³/6 - P·(z - 2)³/6 - q₁·(z - 2)⁴/24 + q₁·(z - 4)⁴/24 - M· (z - 5)²/2

Из условий закрепления по этим уравнениям вычислим начальные параметры:

- начальный угол поворота φ₀ = -994.1 кНм²

- начальный прогиб балки v₀ = 0 кНм³

Найдем углы поворота и прогибы сечений на каждом участке

На участке AB

EJ×φ(0) = -994.1 кНм²

EJ×v(0) = 0 кНм³

EJ×φ(0.5) = -957.5 кНм²

EJ×v(0.5) = -490.9 кНм³

EJ×φ(1) = -847.9 кНм²

EJ×v(1) = -945.3 кНм³

EJ×φ(1.5) = -665.2 кНм²

EJ×v(1.5) = -1327 кНм³

EJ×φ(2) = -409.4 кНм²

EJ×v(2) = -1598 кНм³

На участке BC

EJ×φ(2) = -409.4 кНм²

EJ×v(2) = -1598 кНм³

EJ×φ(2.5) = -132.3 кНм²

EJ×v(2.5) = -1732 кНм³

EJ×φ(3) = 112.8 кНм²

EJ×v(3) = -1736 кНм³

EJ×φ(3.5) = 324 кНм²

EJ×v(3.5) = -1625 кНм³

EJ×φ(4) = 499.3 кНм²

EJ×v(4) = -1418 кНм³

На участке CD

EJ×φ(4) = 499.3 кНм²

EJ×v(4) = -1418 кНм³

EJ×φ(4.25) = 572.9 кНм²

EJ×v(4.25) = -1284 кНм³

EJ×φ(4.5) = 637 кНм²

EJ×v(4.5) = -1132 кНм³

EJ×φ(4.75) = 691.6 кНм²

EJ×v(4.75) = -966.1 кНм³

EJ×φ(5) = 736.8 кНм²

EJ×v(5) = -787.3 кНм³

На участке DE

EJ×φ(5) = 736.8 кНм²

EJ×v(5) = -787.3 кНм³

EJ×φ(5.25) = 770 кНм²

EJ×v(5.25) = -598.8 кНм³

EJ×φ(5.5) = 793.7 кНм²

EJ×v(5.5) = -403.1 кНм³

EJ×φ(5.75) = 807.9 кНм²

EJ×v(5.75) = -202.8 кНм³

EJ×φ(6) = 812.6 кНм²

EJ×v(6) = 0 кНм³