Центр тяжести

Статические моменты площади сечения. Центр тяжести площади сечения

Рассмотрим произвольное поперечное сечение стержня, связанный с координатными осями $XOY$ и выделим элемент площади $dA$ с координатами ($x,y$).

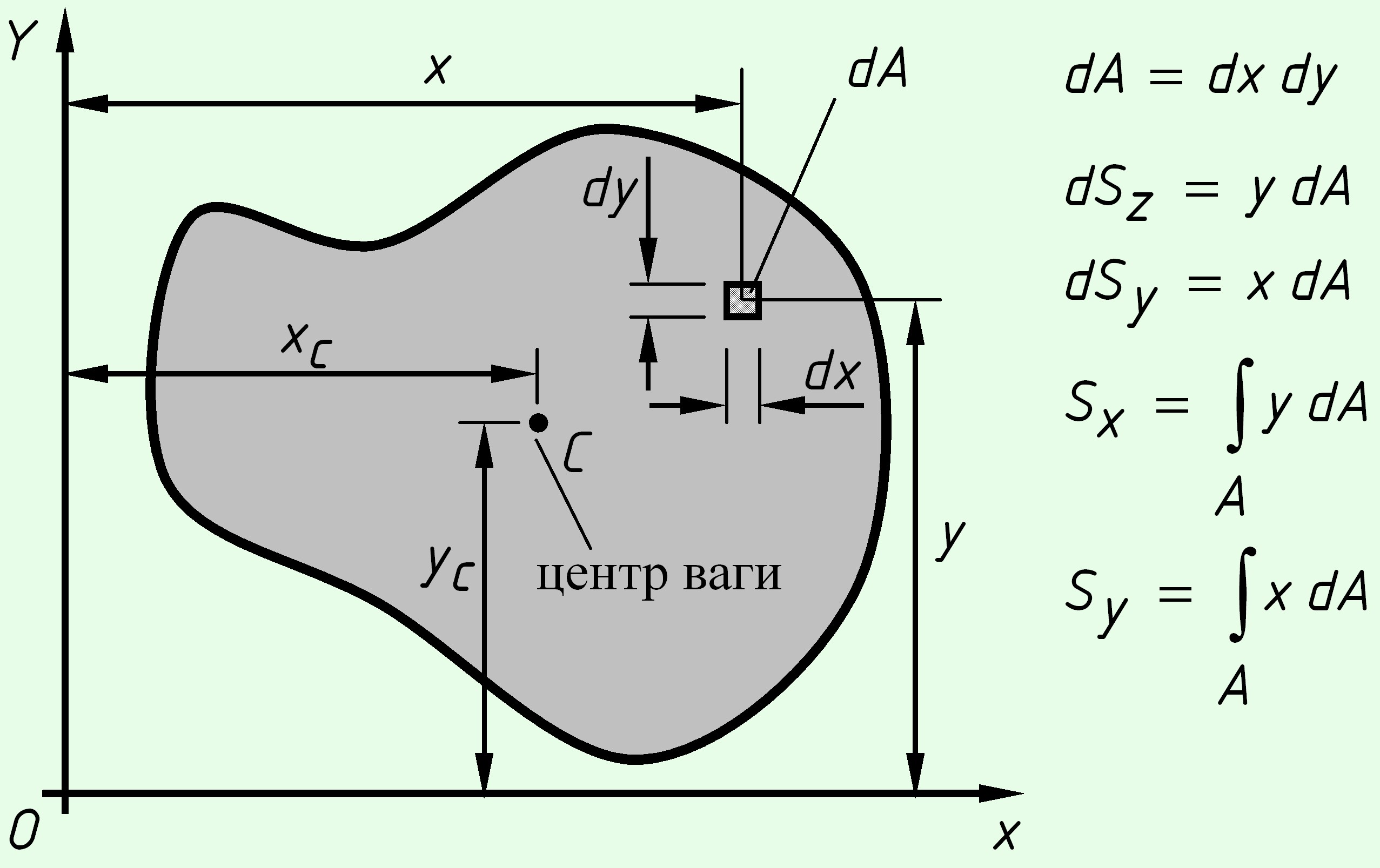
Статическим моментом площади сечения относительно оси называется сумма (интеграл) по всей площади сечения от произведения площади элементарной площадки на расстояние до рассматриваемой оси.

${S_x} = \int\limits_A {ydA} $;        ${S_y} = \int\limits_A {xdA} $ (см3).

Для сечений, для которых известны площади $A$ и координаты центров тяжести ${y_c}$, ${x_c}$, статические моменты площадей рассчитываются по формулам:

${S_x} = {y_c}A$;                ${S_y} = {x_c}A$.                

Статический момент площади сечения может быть положительным, отрицательным и равняться нулю.

Оси, относительно которых статические моменты площади сечения равны нулю, называются центральными.

Примеры определения статических моментов

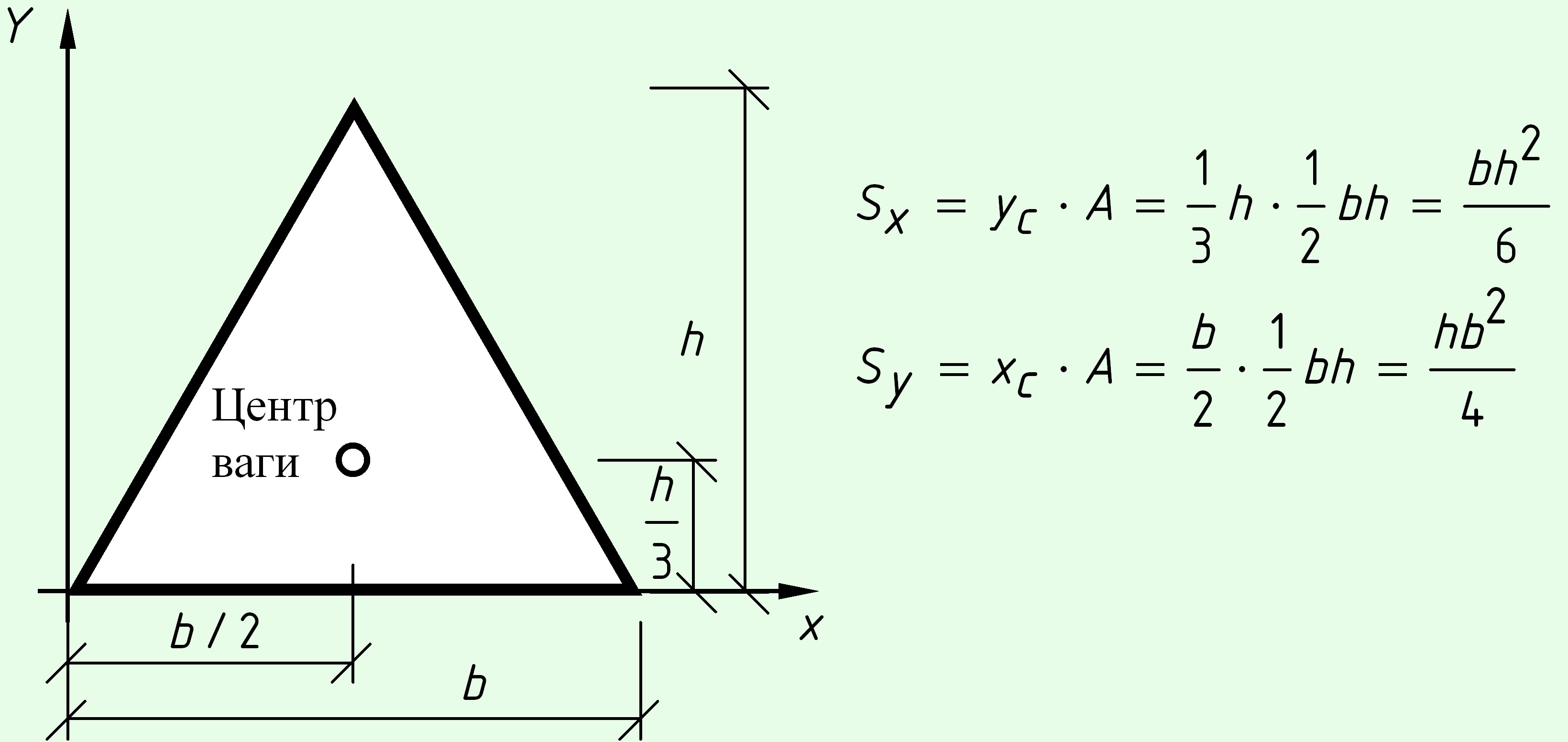
Треугольник.

Поскольку положение центра тяжести треугольника нам известно, его статический момент площади можно определить как произведение площади на соответствующую координату центра тяжести.

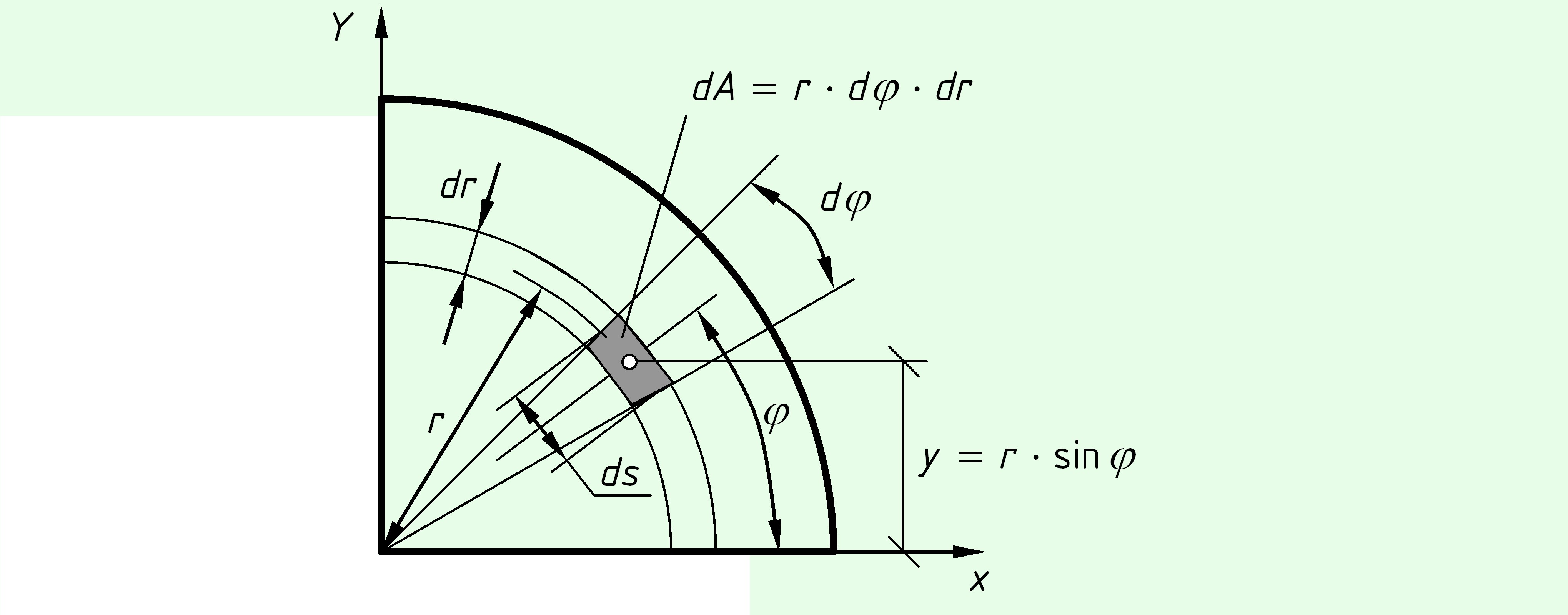
Четверть круга.

Поскольку положение центра тяжести четверти круга мы не знаем, определим статические моменты по общей формуле. Выделим элементарную площадь $dA$ с углом $d\varphi $ и высотой $dr$. Ширина площадки $ds = r \cdot d\varphi \,$.

Статический момент

\[{S_x} = \int\limits_A {ydA}  = \int\limits_0^{\frac{\pi }{2}} {\,\,\int\limits_0^R {r \cdot \sin \varphi  \cdot r \cdot d\varphi  \cdot dr} }  = \int\limits_0^R {\left( {\int\limits_0^{\frac{\pi }{2}} {\sin \varphi  \cdot d\varphi } } \right)}  \cdot {r^2} \cdot dr = \int\limits_0^R {{r^2} \cdot dr}  = \frac{{{R^3}}}{3}\],

где \[\int\limits_0^{\frac{\pi }{2}} {\sin \varphi  \cdot d\varphi }  =  - \left( {\cos \frac{\pi }{2} - \cos 0} \right) =  - \left( {0 - 1} \right) = 1\].

Площадь $A = \frac{1}{4} \cdot \pi {R^2}$.

Координата центра тяжести ${y_c} = \frac{{{S_x}}}{A} = \frac{{4R}}{{3\pi }}$.

Аналогично относительно другой оси ${x_c} = \frac{{{S_y}}}{A} = \frac{{4R}}{{3\pi }}$.

Статический момент составного сечения равен сумме статических моментов его составляющих.

${S_x} = \sum\limits_{i = 1}^n {{{({S_x})}_i}}  = \sum\limits_{i = 1}^n {{y_i} \cdot {A_i}} $;                ${S_y} = \sum\limits_{i = 1}^n {{{({S_y})}_i}}  = \sum\limits_{i = 1}^n {{x_i} \cdot {A_i}} $.

Тогда положение центра тяжести составного сечения запишется так:

${x_c} = \frac{{{x_1} \cdot {A_1} + {x_2} \cdot {A_2} + ... + {x_n} \cdot {A_n}}}{A};\,\,\,\,\,\,{y_c} = \frac{{{y_1} \cdot {A_1} + {y_2} \cdot {A_2} + ... + {y_n} \cdot {A_n}}}{A}$